前言

• 强化学习可以分为有模型和无模型的方法两大类
• 未知模型
  • 学习法
  • 通过智能体的交互，学习值函数和策略
  • 代表方法：MC，TD
• 已知模型
  • 规划法
  • 无需智能体交互，直接从模型学习最优策略
  • 代表方法：DP

基于模型的强化学习

核心思路

• 通过经验，学习出一个虚拟的环境模型
• 利用学到的环境模型，进行动态规划，计算价值函数或者策略

优势

• 可以通过监督学习，有效地学习环境模型
• 可以将学到的环境模型放在GPU内，快速得到大量的交互信息
• 没有任何真实损失
• 直接利用环境模型的不确定性

劣势

• 先学环境模型，再学值函数，存在两次近似误差 -> 累计误差

Dyna-q

• 算法流程
  • 
  • repeat n times的部分实际上是在用学习到的虚拟环境模型进行学习，这一部分可以新开一个线程，和外面真实的环境交互分开。
  • 真实的环境交互1秒一次，而计算机中虚拟的环境交互0.1秒一次，那这里的n就是10。

蒙特卡洛树搜索Monte-Carlo Tree Search

• 特性

  • 适用于Combinatorial Games
  • Combinatorial Games特点：零和、完美信息、确定性、离散、序列化

• 算法核心

  • 在MCTS中，仿真策略需要策略提升
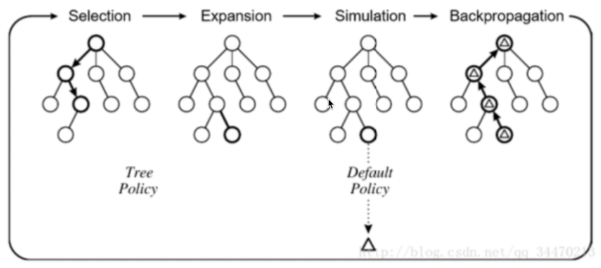
  • 每次仿真有两个阶段
    • 树策略(提升)：选择动作，最大化Q(S, A)
    • 默认策略(固定)：快速计算到终止状态
  • Repeat(每次仿真)
    • 使用MC评价来估计Q(S, A)
    • 提升树策略，比如epsilon-贪婪，UCB等
  • 对仿真出来的经验做MC优化
  • 搜索到最优的搜索树Q(S,A)->q*(S,A)

    epsilon-贪婪对于非最优策略是均匀采样的 UCB既考虑了值函数，又考虑了探索的次数 = 回报值/仿真次数

• 优势

  • Highly selective best-first search
  • 动态评价状态
  • 结合了采样去打破维度诅咒，用采样取代了暴力搜索
  • 适合于各种黑盒模型，不需要满足马尔可夫性
  • 计算有效，容易并行

• 算法流程

  • 
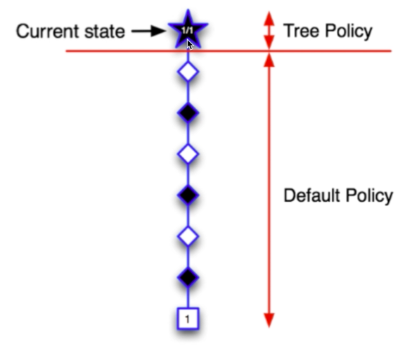
    • 当前状态S1为叶子节点，直接从当前状态开始，用默认策略进行仿真
    • 结果“赢了”
    • 更新节点的UCB=获胜次数/仿真次数
  • 
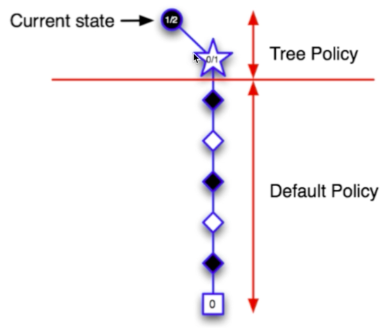
    • 依据UCB规则选择一个动作向下走，每一个动作都对应了一个UCB
    • UCB其实是一个值，与值函数正相关，与仿真次数负相关
    • 但是目前仿真次数都是0，所以根据值函数选一个动作，到达S2
    • 结果“输了”
    • 更新树策略路径上的每个节点的UCB
  • 
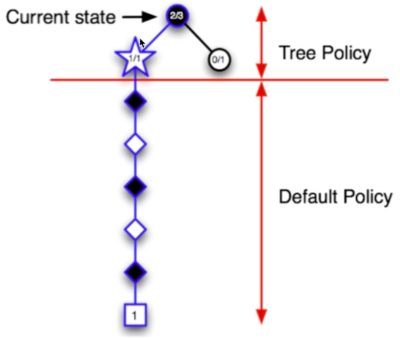
    • 从S1开始，根据UCB选一个动作
    • 由于第二步中，最终结果是“输了”，所以第二步中动作的UCB下降了，于是从S1重新选一个动作，到达S3
    • 结果“赢了”
    • 更新树策略路径上的每个节点的UCB
  • 
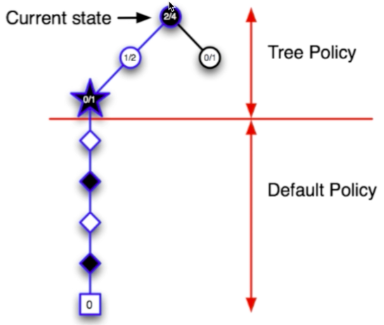
    • 再从S1开始搜索，搜到S3后，再选一个动作，到达S4
    • 结果“输了”
    • 更新树策略路径上的每个节点的UCB
  • 
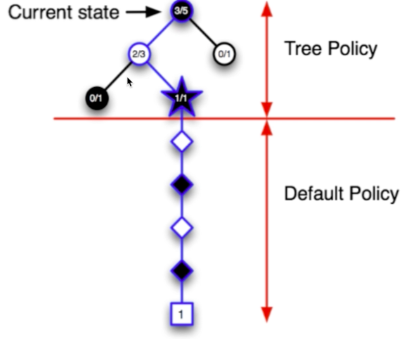
    • 再从S1开始搜索，搜到S3后，没有去S4(因为S4刚刚输了，UCB下降)，再选一个动作，到达S5
    • 结果“赢了”
    • 更新树策略路径上的每个节点的UCB

  • 后面的步骤依次类推

  • 

TD搜索

• 算法特性

• 有些情况下，没有终止状态，MC方法不适用
• 将MCTS中的MC评价换成TD评价

• 算法流程

  • 从当前状态St开始采样片段
  • 估计Q(s, a)
  • 对于每一步的仿真，使用Sarsa方法更新Q函数
    • 
  • 基于Q(s, a)选择动作