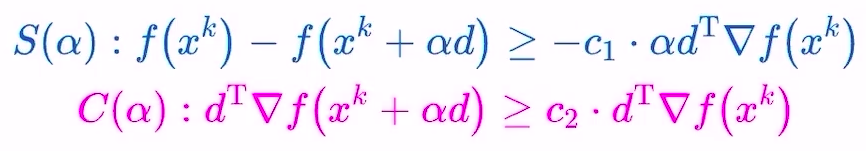Newton’s Method

牛顿法

前提条件
- 一阶导和二阶导连续
- 具有严格正定的Hessian矩阵
原理
- 对函数进行二阶泰勒展开
  - $f(x)\approx f(x_{k})+\triangledown f(x_{k})^{T}(x-x_{k})+\frac{1}{2}(x-x_{k})^{T}\triangledown ^{2}f(x_{k})(x-x_{k})$
- 导数为0时得到极值点
  - $\triangledown f(x)=\triangledown ^{2} f(x_{k})(x-x_{k})+\triangledown f(x_{k})=0$
  - $x=x_{k}-\left [ \triangledown ^{2}f(x_{k}) \right ]^{-1}\triangledown f(x_{k})$
- 更新公式
  - $x_{k+1}=x_{k}-\left [ \triangledown ^{2}f(x_{k}) \right ]^{-1}\triangledown f(x_{k})$
  - 减号后面的内容就是牛顿步长（Newton step），这里需要满足Hessian严格正定 $\triangledown^{2} f(x_{k})>0$ ，因为沿着梯度的负方向才可以保证函数值下降，牛顿步长是一个负号乘Hessian的逆再乘梯度，Hessian的逆必须要和梯度是同向的（正定）才行，从而Hessian也必须是正定的
- 特别的，如果目标函数本身就是二次的，那一步就可以迭代到最优解
与梯度下降法对比
- 下降路线更加平直
- 迭代次数更少
- 每次迭代计算量更大
缺点
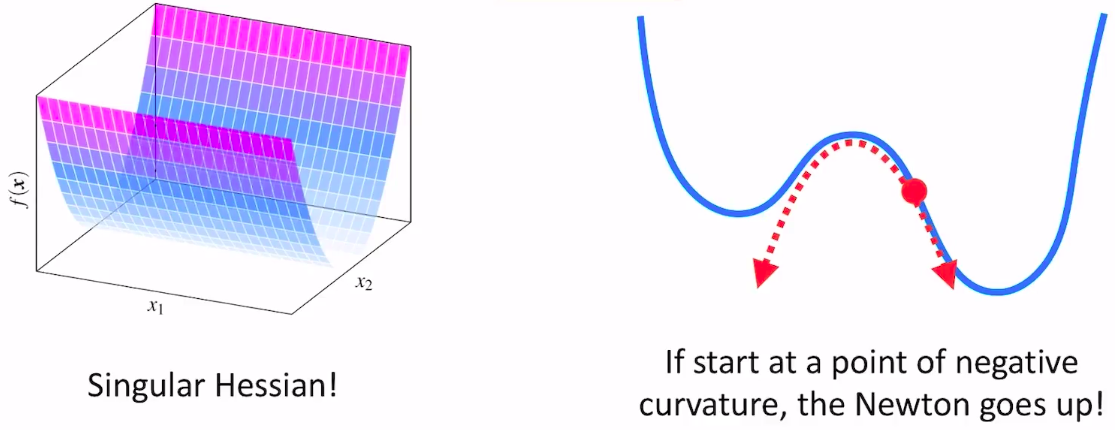
- 很多时候Hessian矩阵是半正定或者不定的，会导更新方向不是梯度的反方向，函数值增大

Damped Newton’s Method

阻尼牛顿法

当初始点距离最优解较远时，Hessian不一定正定，迭代不一定收敛，因此引入步长因子
- $d=-H^{-1}g/$
- $x_{k+1}=x_{k}+td_{k}$

Modified Newton’s Method

修正牛顿法

背景
- 提高牛顿方法在一般函数上的鲁棒性
- 对牛顿法的优化思路
  - 考虑到Hessian不一定正定，尝试用一个正定的 $M$ 拟合Hessian，只要拟合的够接近，也可以近似表示曲率信息
  - 其实没必要求 $M^{-1}$ ，本质上我们是想求线性方程 $Md=-\triangledown f(x)$ 的解 $d$ ，可以用一些成熟的线性求解器进行求解，比解逆快很多
  - inexact line search不需要求Hessian，梯度也只是在最开始算一次，更新 $t$ 的过程中不需要计算梯度，所以计算量很小
原问题
- $\left [ \triangledown ^{2}f(x) \right ]d=-\triangledown f(x)$
用拟合Hessian
- 如果是凸函数（Hessian半正定）
  - $M=\triangledown ^{2}f(x)+\epsilon I,\epsilon =min(1,\left\| \triangledown f(x) \right\|_{\infty })/10$
  - $M$ 严格正定，搜索方向的求解可以用Cholesky factorization快速求解
  - $Md=-\triangledown f(x),M=LL^{T}$ ， $L$ 是个下三角矩阵
- 如果是非凸函数（Hessian不定）
  - 将Hessian进行Bunch-Kaufman Factorization，原问题转化为 $LBL^{T}d=-\triangledown f(x)$
  - 其中， $L$ 是个下三角矩阵， $B$ 是个对角线由 $1\times 1$ 和 $2\times 2$ 的矩阵块组成的块对角阵
  - 的标量一定是正数，的矩阵块的特征值是一正一负，我们需要把每个矩阵替换为和其最接近的正定矩阵，最终得到新的（正定），把求解出来
    - 上面 $2\times 2$ 矩阵的正定化就是把负的特征值都算出来，然后用一个 $\epsilon$ 去代替负特征值得到新的矩阵
缺点
- 仅仅保证了Hessian的正定，还是要把Hessian求出来，计算量大

Quasi Newton’s Method

拟牛顿法

牛顿法的问题
- 牛顿法需要函数在任何点的Hessian可逆且正定，条件比较苛刻
- 牛顿法的计算量太大
- 当 $x$ 距离函数的最优解还比较远的时候，用二次函数进行近似的效果不好，这时候用牛顿法不仅计算量大，收敛还很慢；当 $x$ 距离函数的最优解比较近的时候，二次函数的近似会好一些，收敛会很快。
- Hessian拟合的函数的条件数可能会变得很大（poorly conditioned）。比如函数是一段直线和一段二次曲线拼接起来的，在直线部分计算Hessian去确定更新步长的话，会得到一个非常大的更新步长（曲率是0，对0取逆是无穷大）
拟牛顿法需要满足的一些特质
- 原理和修正阻尼牛顿法一样，设计一个 $M$ 去近似 $H$
- 收敛速度应该在牛顿法和最速梯度下降法之间
- 不需要计算完整的Hessian矩阵（低计算量）
- 线性方程 $Md=-\triangledown f(x)$ 存在闭式解
- $M$ 不应该是一个稠密的阵，只需要在重要的的方向上对 $H$ 做近似，尽可能稀疏
- $d$ 一定得让函数下降（和梯度方向的夹角小于90度），其实就是 $M$ 必须正定
- $d$ 应该包含曲率信息（收敛要比梯度下降来的快），也就是满足 $\Delta g\approx M^{k+1}\Delta x$
拟牛顿法的核心思路
- 通过采样N对 $\Delta x$ 和 $\Delta g$ 来估计 $\Delta M$
- 同时，考虑到最终是要求 $M^{-1}$ ，干脆直接估计 $B=M^{-1}$ ，更新方向 $\Delta x=B\Delta g$
- 估计 $B$ 的时候避免计算Hessian矩阵

凸且光滑函数的BFGS方法

假设我们有了很多的和，怎么估计B呢？还是用优化迭代的思路：
- 初始化 $B^{0}$ 为单位阵
- 迭代求解最优的，迭代的思路如下：
  - 我们希望迭代前后B的差距尽可能小： $min_{B^{k+1}}\left\| B^{k+1}-B^{k} \right\|^{2}$
  - 其次，需要满足一些约束：
    - $B=B^{T}$ ，这是因为Hessian是对称阵，所以Hessian的逆也应该对称
    - $\Delta x=B\Delta g$
  - 注意，单纯用差的二范数描述 $B^{k}$ 和 $B^{k+1}$ 的变化并不好，比如 $\begin{bmatrix} 100 & 1 \\ 1 & 100 \\\end{bmatrix}$ 和 $\begin{bmatrix} 100 & 0.5 \\ 0.5 & 100 \\\end{bmatrix}$ 的差值的二范数很小，但对于右上和左下角的元素来说变化和其自身的大小相比是巨大的，因此需要进行归一化
  - 归一化后，优化目标变成： $min_{B^{k+1}}\left\| H^{\frac{1}{2}}(B^{k+1}-B^{k})H^{\frac{1}{2}} \right\|^{2}$ ， $B=H$ 为真实的Hessian矩阵， $H=\int_{0}^{1}\triangledown^{2}f\left[(1-\tau)x^{k}+\tau x^{k+1}\right]d\tau$
  - 我们本来就是套估计H，现在这里还要用到H，看起来是个鸡生蛋，蛋生鸡的问题，但实际上这个问题是有解析解的，与 $H$ 无关。四个优化领域的大佬提出了BFGS方法，最终得到的更新公式如下：
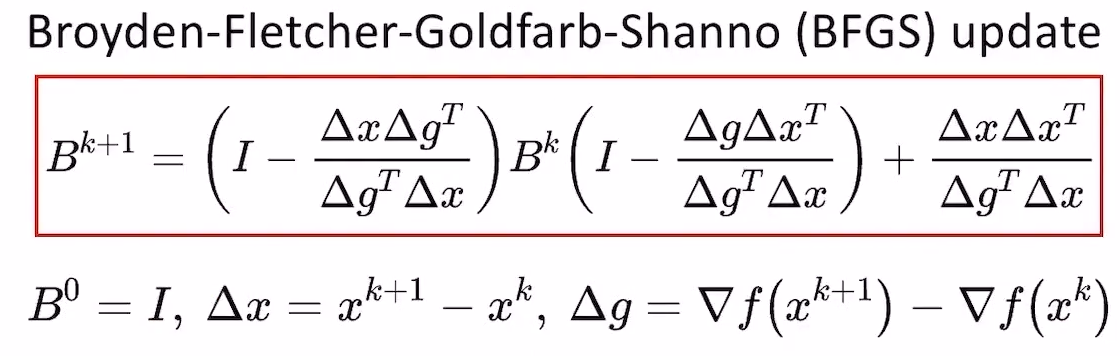
  - 注意：当 $\Delta g^{T}\Delta x>0$ 时，我们可以保证BFGS更新的结果是正定的，从而保证 $\Delta x$ 的方向是函数值下降的方向，对凸函数而言，这是绝对成立的（可以回顾强凸性的定义）；非凸函数后面讨论
适用于凸且光滑函数的BFGS方法的流程
- $g$ 是梯度
- $d$ 是更新方向
- $t$ 是line search方法确定的步长
缺点与问题
- 严格梯度单调性（严格凸函数）的条件过于苛刻，一般函数很难满足
- 曲率的计算在optimum附近有效，在远处反而是浪费算力
- 每次迭代的计算复杂度是优化变量的维度的平方，还是不够轻量
- 在非凸函数上是否能够保证收敛仍未知
- 在非光滑函数上能否正常使用仍未知

非凸但光滑函数的BFGS方法

在非凸函数上如何保证，从而保证更新方向是函数值的下降方向呢？答案是线搜索的时候满足Wolfe conditions
- weak wolfe conditions
  - sufficient decrease condition保证了函数值的下降
  - curvature condition保证了这一步跨的足够大，从下山跨到上山
- strong wolfe conditions
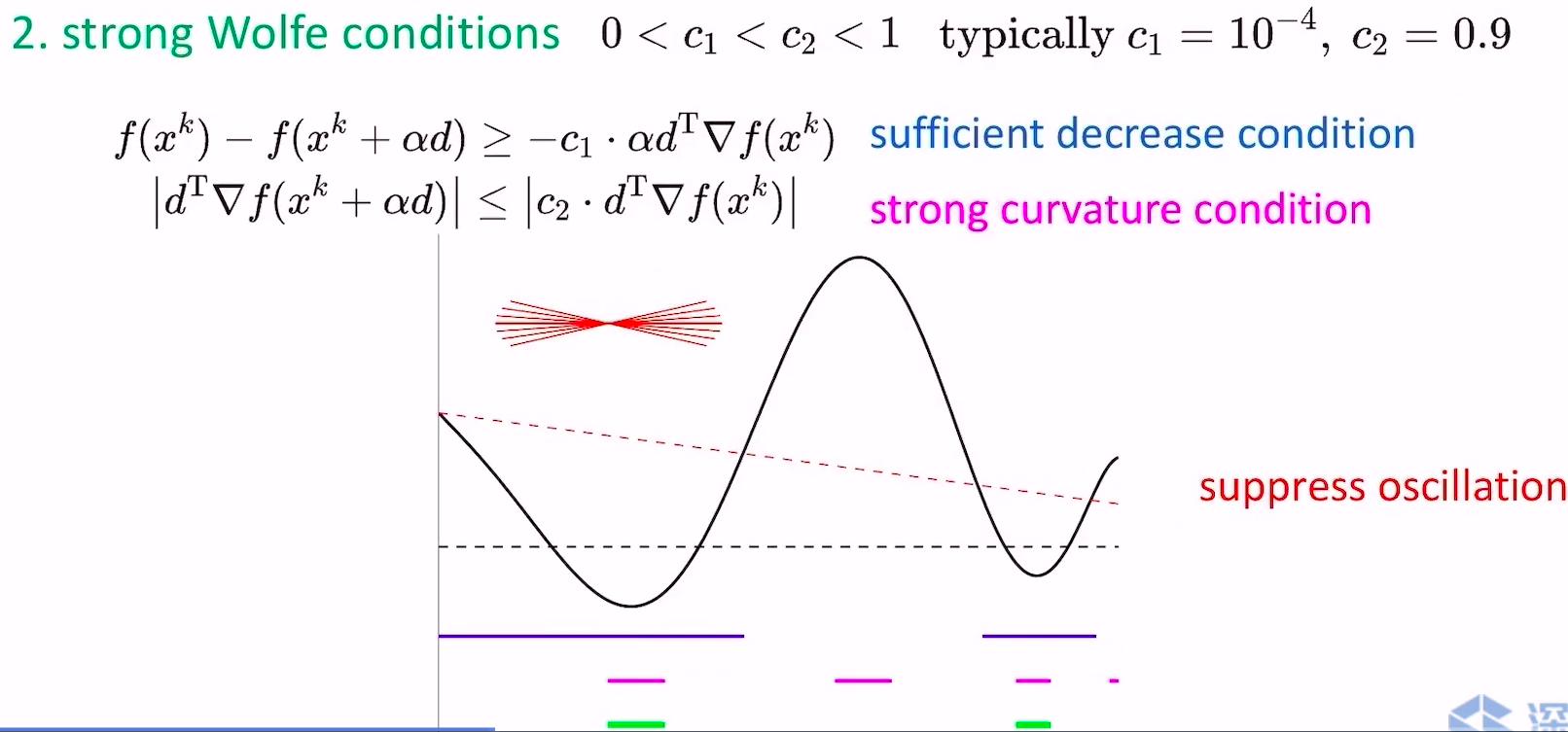
  - strong和weak的区别在于对curvature condition加了个绝对值约束，不让这一步跨的太过头（跑到对面的山坡上），可以抑制震荡
但Wolfe conditions只能保证方向是下降方向，如何保证BFGS的收敛性呢？答案是cautious update(Li and Fukushima 2001) with mild conditions
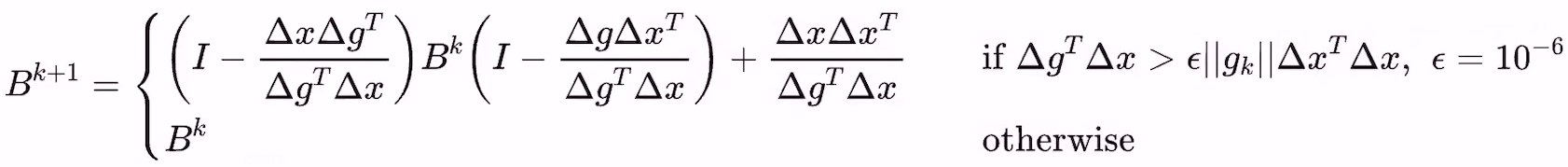
- 只要函数满足如下两个条件，cautious update都可以保证BFGS的收敛性
  - 函数有bounded sub-level sets
  - 函数有lipschitz continuous grad
适用于非凸但光滑函数的BFGS方法的流程
与牛顿方法的收敛速度对比
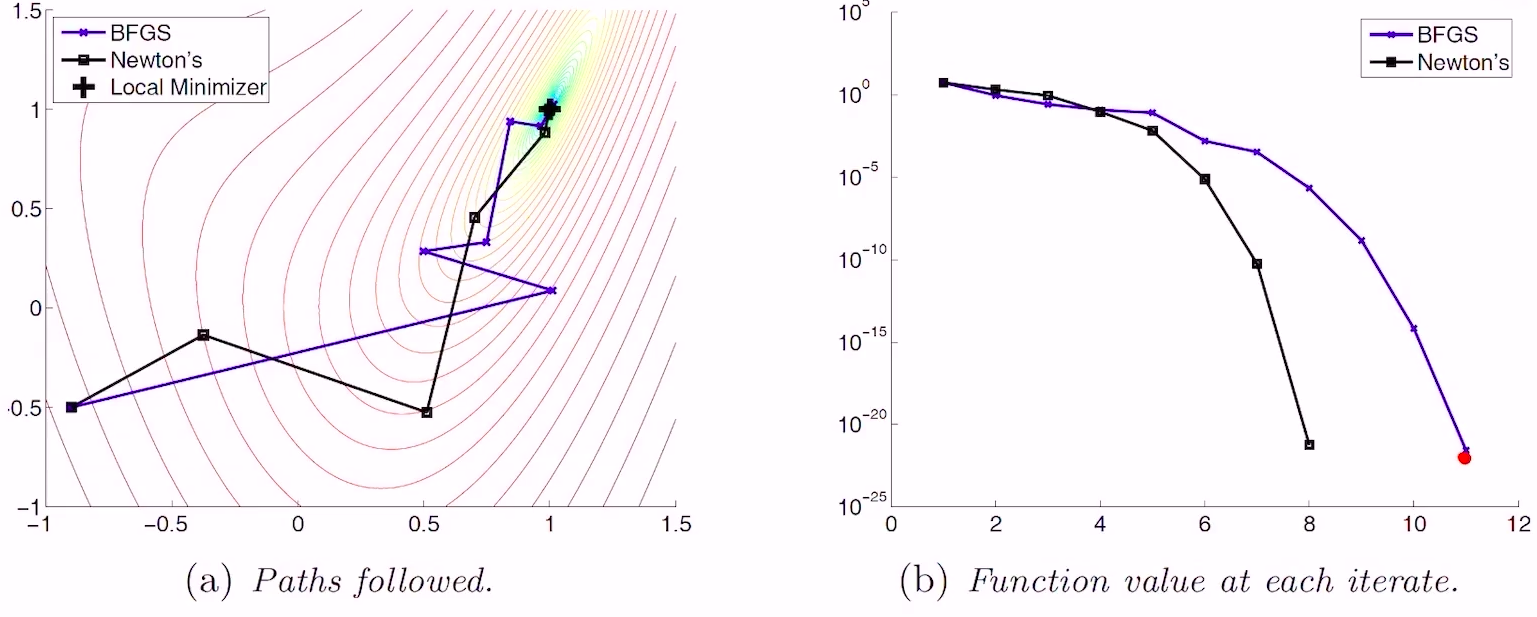
- 速度上慢了一点点，但计算量少很多，综合看更具优势

Limited-memory BFGS(L-BFGS)方法

由于 $B^{k+1}$ 是由 $B^{k}$ 迭代计算得到的。所以 $B^{k}$ 隐含了 $B^{k-100}$ 的信息。但直觉上来说， $x^{k}$ 和 $x^{k-100}$ 已经差的很远了， $x^{k-100}$ 处的曲率信息对 $x^{k}$ 处的曲率信息的推导没有啥有效价值了，因此我们可以设置一个memory buffer，让 $B^{k-m}$ 到 $B^{k-1}$ 来决定 $B^{k}$ 的取值，从而降低计算量。
L-BFGS方法的流程
- 就是把上面的Cautious-BFGS过程改成下面的 $B^{k}$ 更新流程
- 上图左边方法的复杂度是 $O(mn^{2})$ ，因为每个window size内的信息都被重复遍历并计算了。实际上每个循环中，我们只需要将窗口中的头元素去掉，末尾的新元素算进来即可，因此改成右边的计算过程后可以将复杂度简化到 $O(mn)$ ，具体推导可以看Liu and Nocedal 1989.
与Newton和BFGS的对比
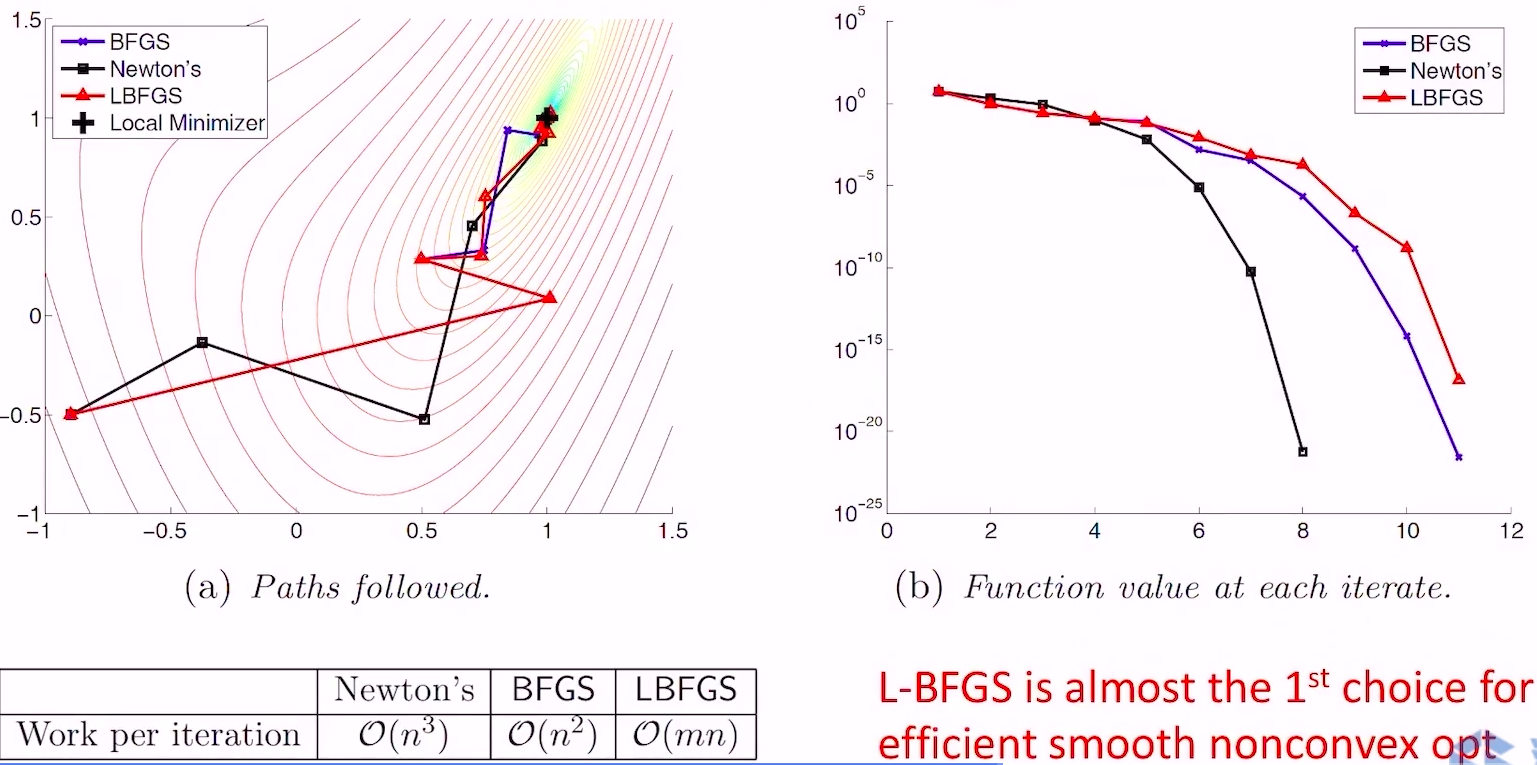
- 由于牺牲了部分历史信息，收敛速度相比BFGS更慢一些，但计算量从 $O(n^{2})$ 降低到 $O(mn)$ ，当 $n$ 很大的时候，效率提升就非常大了，基本上是光滑非凸函数优化的第一选择

非凸且非光滑函数的L-BFGS方法

wolfe conditions方法选择
- 假设我们把strong wolfe conditions方法直接应用在非凸且非光滑函数上，看看会发生什么
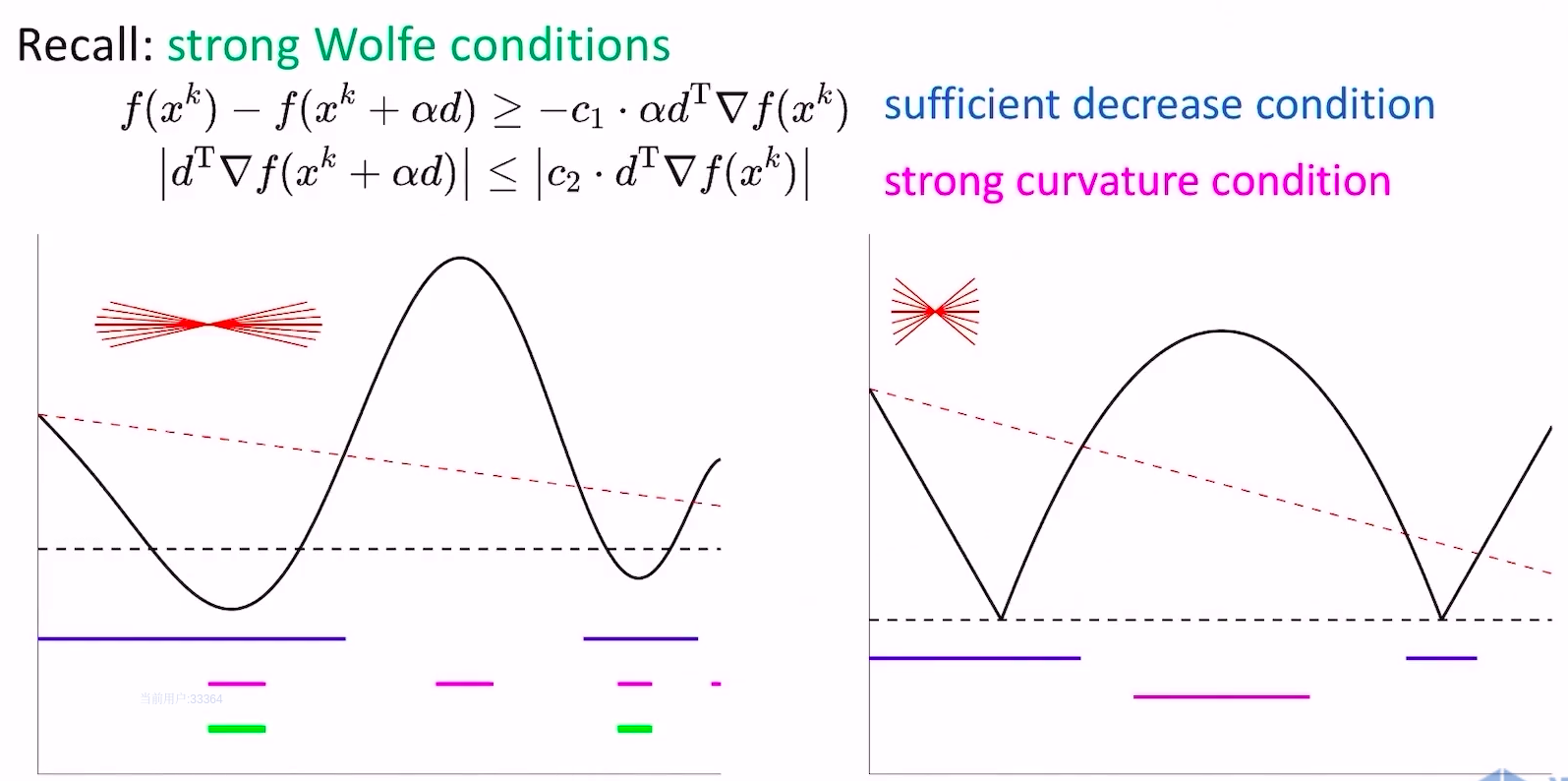
  - 回顾一下，strong wolfe conditions通过绝对值约束，将更新点的梯度压在0附近，但上图右侧的非光滑函数没有任何点的梯度在0附近，导致无法找到满足strong wolfe conditions的点
- 假设我们把weak wolfe conditions方法直接应用在非凸且非光滑函数上，看看效果
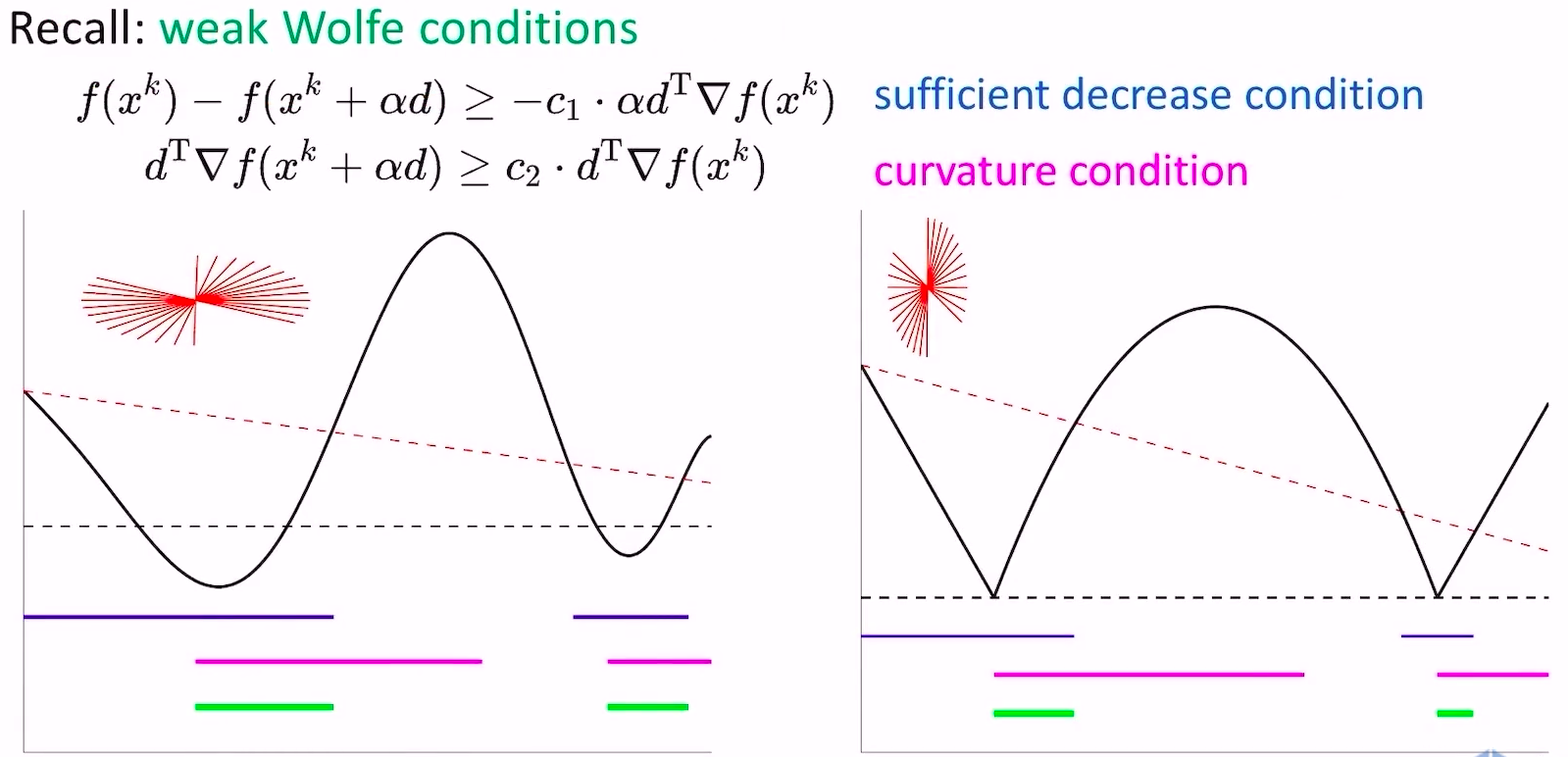
  - weak wolfe conditions方法可以保证能找到满足条件的更新点
- 结论：使用weak wolfe conditions方法处理nonsmooth函数
如何确定一个步长使得weak wolfe conditions被满足呢？
- 对smooth函数，用拟合法确定步长
  - 先初始化一个步长 $\alpha$
  - 如果该步长满足weak wolfe conditions，直接返回
  - 如果不满足weak wolfe conditions，根据 $\left ( x,{f}\ '(x) \right )$ 和 $\left ( x+\alpha d,{f}\ '(x+\alpha d) \right )$ 两个点去拟合二次函数，取二次函数的极值点作为新的步长，不断迭代，直到满足weak wolfe conditions
  - 但是当函数nonsmooth（或者条件数很大）的时候，这种二次函数拟合的效果很差，导致求出来的极值点也很不理想，就不再适用了
- 对nonsmooth函数，用Lewis & Overton line search方法
注意点
- $x_{0}$ 一定要取在可导的点，不能一上来就落在nonsmooth处
非凸且非光滑函数的L-BFGS方法流程