Low-Dimensional Linear Program

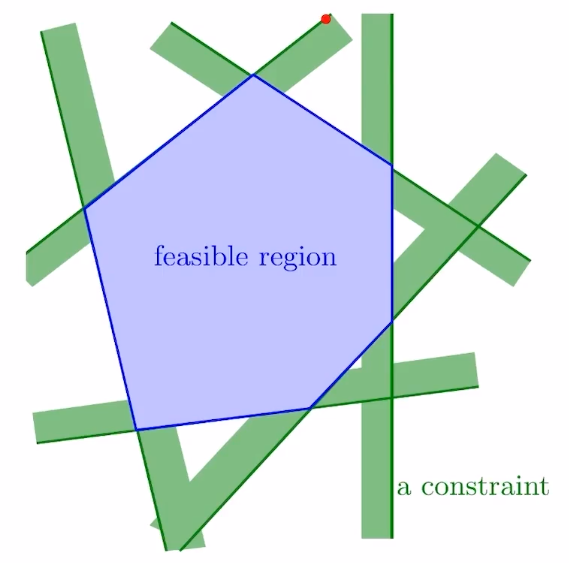
问题形式
- 其中的 $d$ 特别的小，但c $n$ 可以很大
几何上的理解
相关方法对比
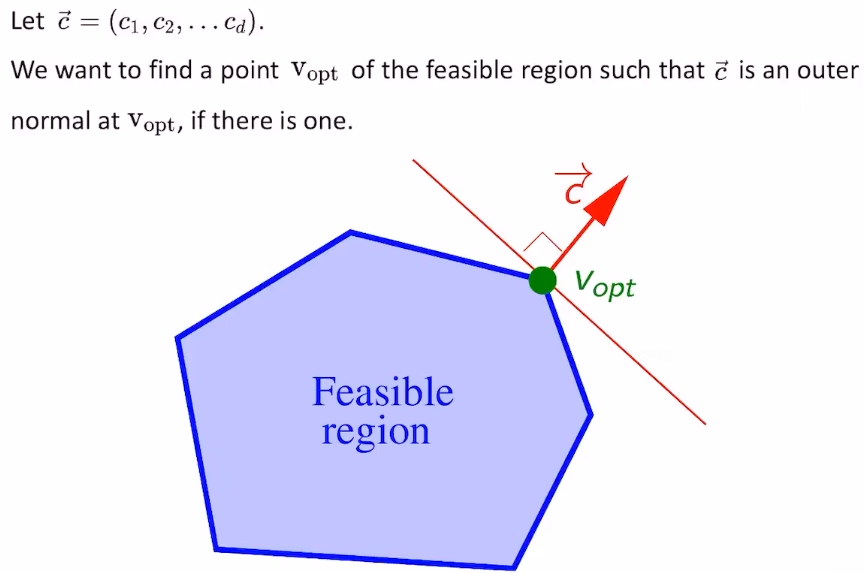
- the simplex algorithm
  - 能得到精确解，但最坏复杂度是指数时间的
  - GLPK用的是simplex方法解LP
- IPM
  - 复杂度是多项式时间，但不能得到精确解
- Seidel’s Algorithm
  - 在低维、高约束量的前提下，具备线性时间复杂度，精确解的优势
Seidel’s Algorithm流程
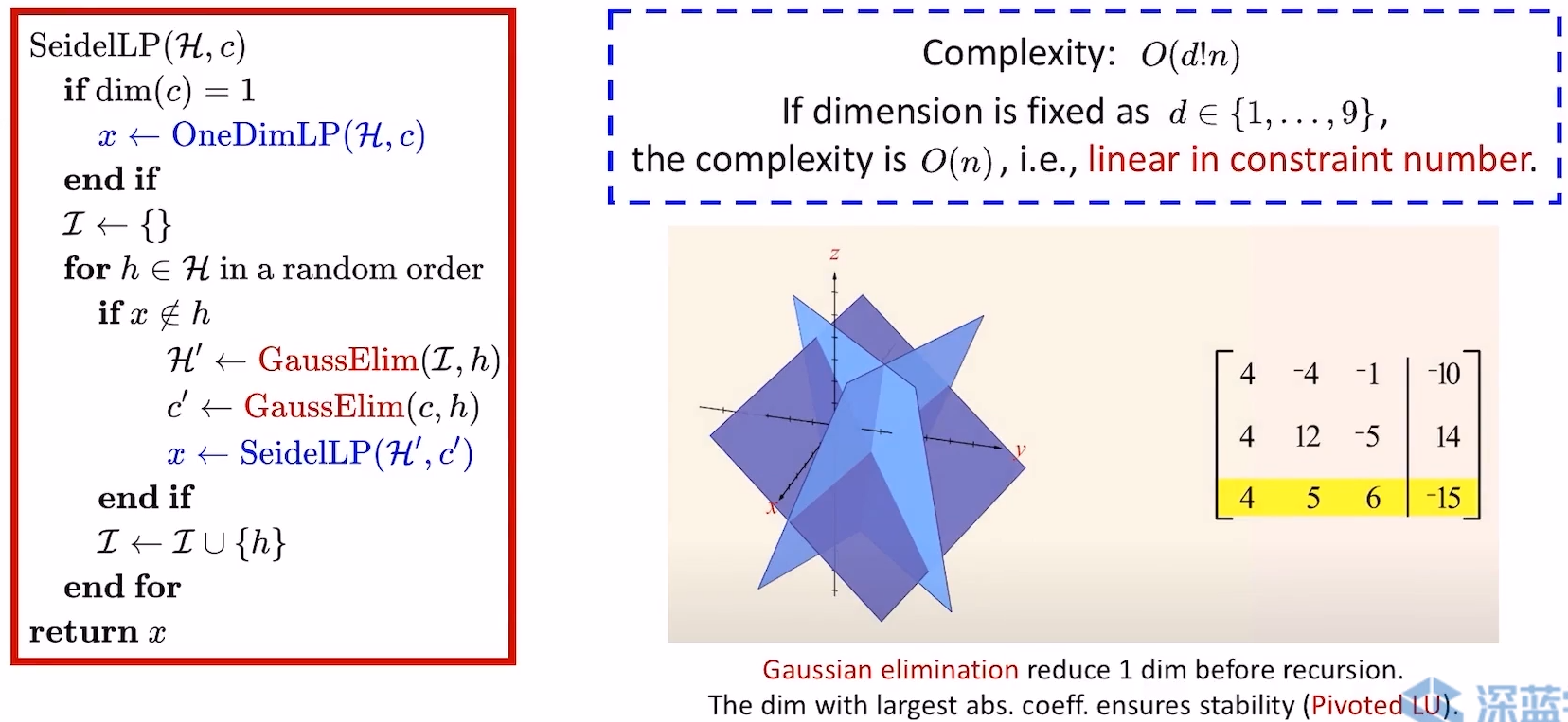
- random order可以通过Fisher-Yates方法生成
- 高斯消元本质是将 $dim$ 降维成 $dim-1$ 。
- 高斯消元的时候，每次选择系数的绝对值最大的元去消，可以保证算法的数值稳定性。从几何上理解，对于平面 $ax+by+cz=d$ 来说，如果 $z$ 的系数的绝对值最大，说明平面和z轴最垂直（和xy平面最平行），将z消去后，信息损失很少。
Seidel’s Algorithm应用
- Linear Separability(点集碰撞检测)
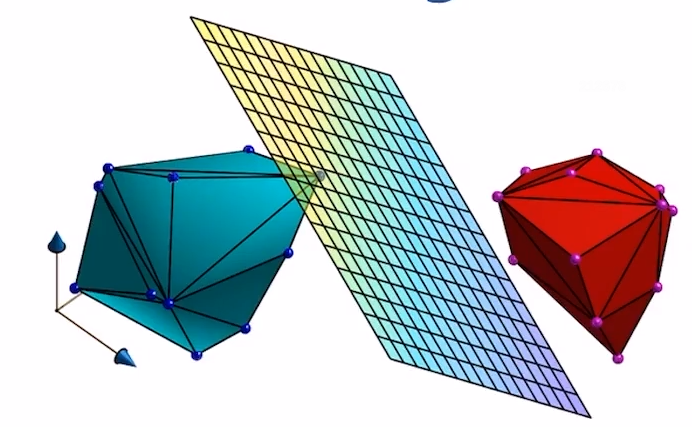
  - 本质上是找一个超平面，使得绿色点集中的所有点在超平面的一侧，红色点集中的所有点在超平面另一侧
- Chebyshev Center(切比雪夫中心)
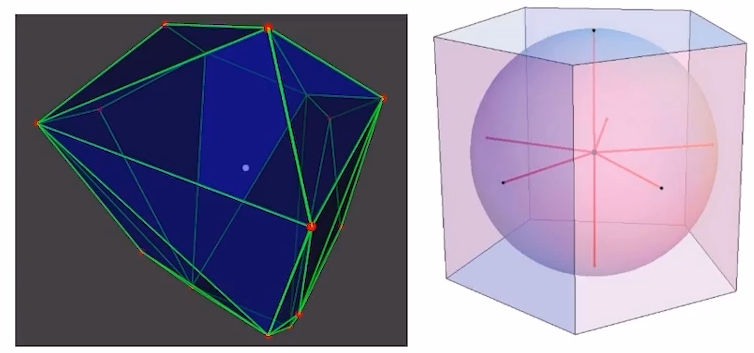
  - 本质上是找一组超平面的最大内切圆，圆心即距离所有边都最远的点
  - 假设这组超平面为 $Ax\leq b$ ，其中 $A=\left [a_{1}^{T},a_{2}^{T},...,a_{m}^{T}\right]^{T}$ ， $b=\left [b_{1},b_{2},...,b_{m}\right]^{T}$ ，假设 $\left\|a_{i}^{T}\right\|=1$ ，那这里的 $a_{i}^{T}$ 就是第 $i$ 个超平面的单位法向量
  - 由于球在超平面内部，所以球上的每个点都满足 $Ax\leq b$ ;为了让点距离每个超平面都最远，我们引入一个margin $y$ ，我们在保证 $Ax+y\leq b$ 的同时，让 $y$ 尽可能大
  - 写成向量形式就是 $min_{\bar{x}\in R^{n+1}}-\bar{x}^{T}e_{n+1},s.t.(A,1)\bar{x}\leq b$ ，其中 $\bar{x}=(x^{T},y)^{T}$ ， $e_{n+1}=(0,...,0,1)^{T}$
- 利用切比雪夫中心进行凸包碰撞检测
  - 已知一个凸包为 $A_{1}x\leq b_{1}$ ，另一个凸包为 $A_{2}x\leq b_{2}$ ，联立组成新的凸包， $\begin{bmatrix}A_{1}\\A_{2}\end{bmatrix}x\leq \begin{bmatrix}b_{1}\\b_{2}\end{bmatrix}$ 并求新凸包的切比雪夫中心，如果有解，则说明两个原凸包有交集

朝花夕拾

Low-Dimensional Linear Program

Low-Dimensional Linear Program

Search

欢迎添加我的微信

Table of Contents