基础

• 推荐书籍
  • Practical Augmented Lagrangian Methods for Constrained Optimization
    • 非常重要的一本书
  • Randomized Algorithms
    • 主讲Low-Dim精确算法，用Randomize降低算法的复杂度
• 约束优化的问题形式
  • 
  • 
  • 
• 常见的约束优化形式
  • 
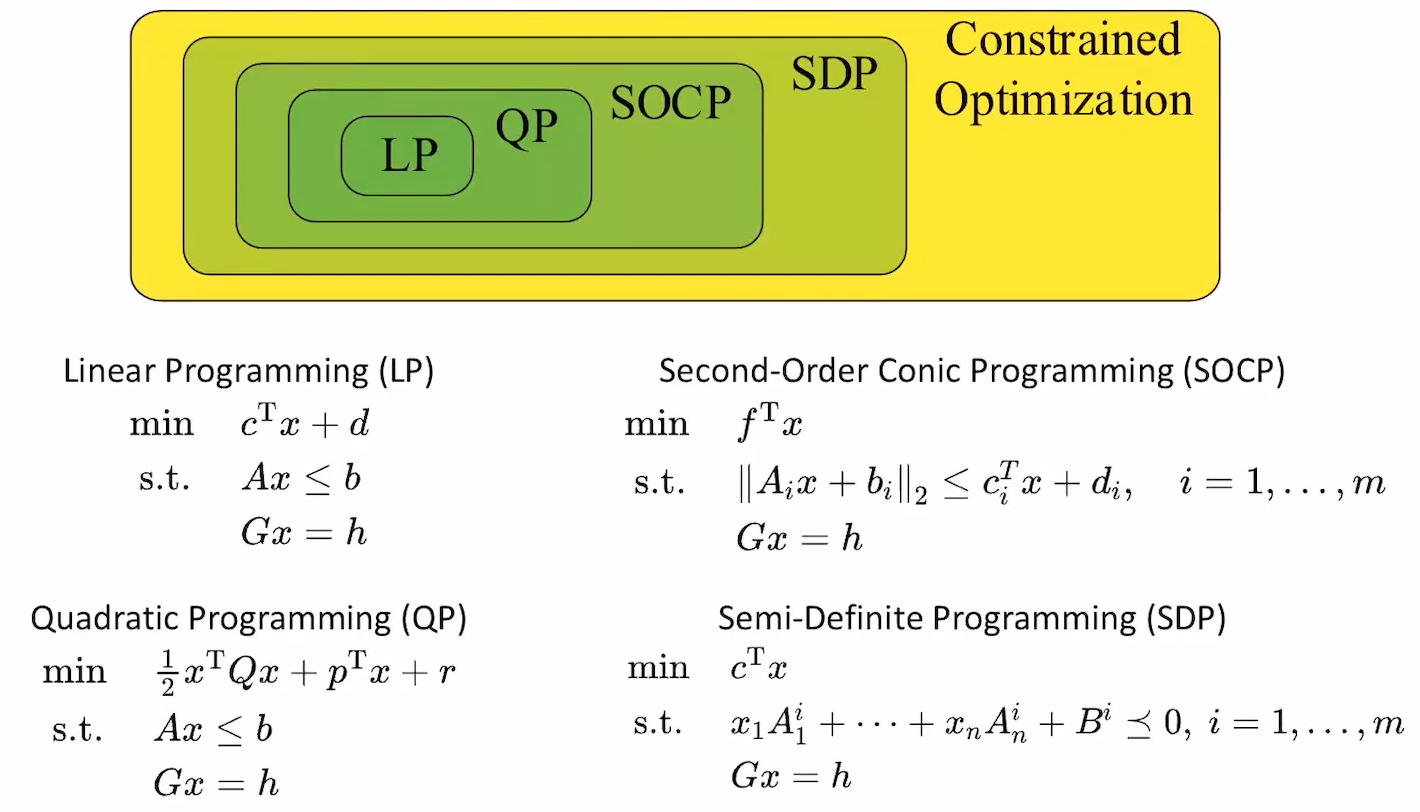
  • 各自的复杂度
    • 
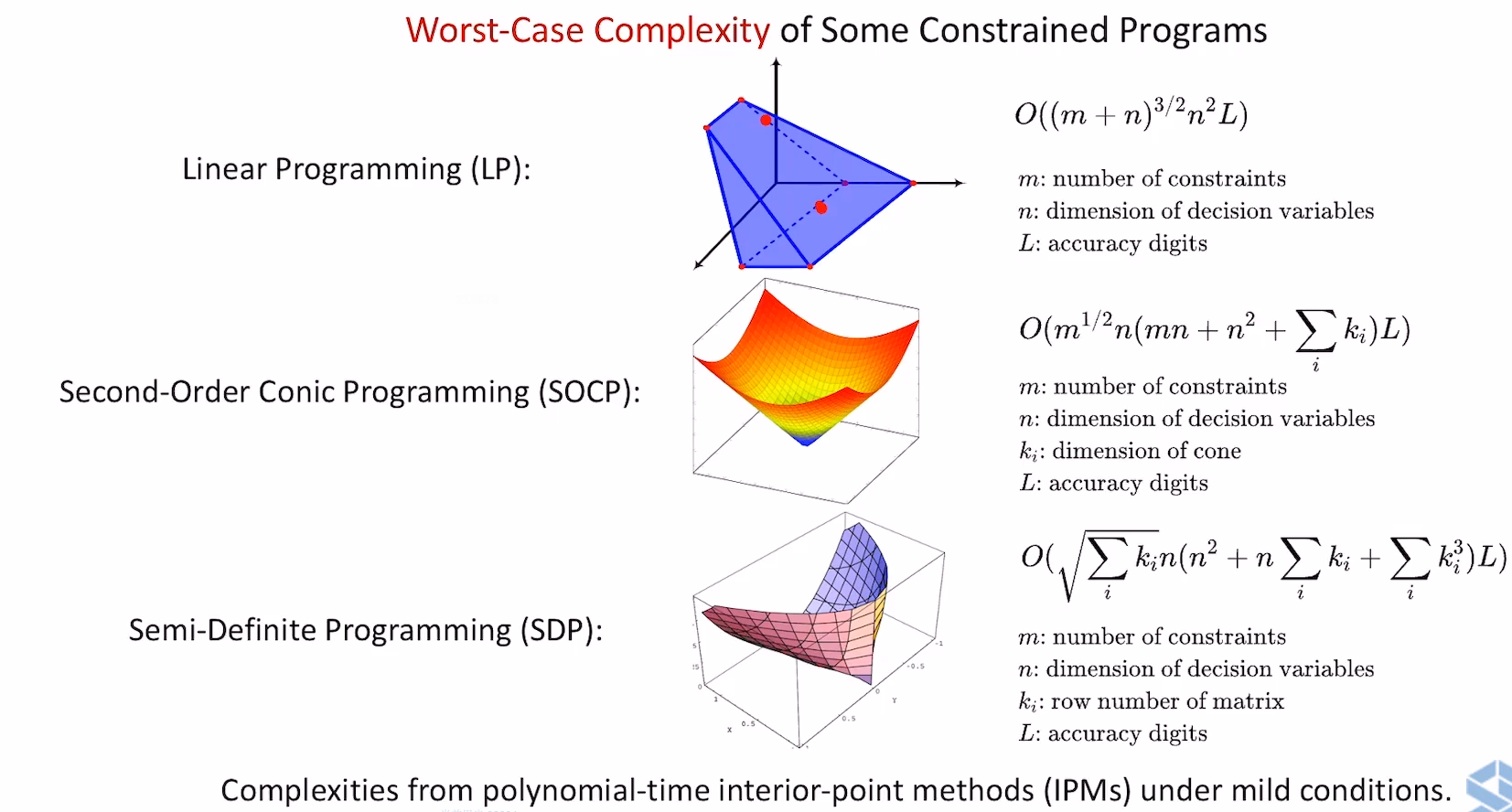
    • 考虑方法的时候不是要考虑理论复杂度最低的，而是要根据问题特性考虑最合适的
• 约束优化方法的分类
  • Approximation algorithm：无法得到精确解，解的精度下降到一定程度就停止了
    • Newton
    • L-BFGS
  • Exact algorithm：可以在有限迭代次数以内达到精确解
    • Simplex（LP、QP）
  • 常用的都是Approximation algorithm，Exact algorithm是非常奢侈的，依赖我们对问题在几何上的理解
• 常见的约束优化方法
  • IPMs（内点法）
    • 的特点
      • 如果一般需要次迭代
      • 在所有被证明了复杂度的方法里实用性最高的
      • 虽然IPM的迭代次数是但每次迭代的计算复杂度是quadratic/cubic（），计算非常稠密，所以不适合解大规模问题
      • 有些IPM的实现用了sub-dual embeding的方法，可以判断LP/SOCP/SDP是否是infeasible的
      • 精度相对比较高，速度相对慢
      • IPM有很多的工程实现
        • Ecos
        • MOSEK：擅长锥规划
        • Gurobi：在QP问题上实现了稳定的IPM方法
        • HPIPM：实时性很高，从汇编开始优化线性求解器
    • 有些情况下IPMs不是最好的选择
      • dim或constrain size很大
      • Hessian unavailable
      • 求解精度不需要很高
      • 求解精度需要非常高（精确解，迭代方法难以满足要求）
      • 高频解小问题
  • OSQP底层是ADMM，属于一阶方法
  • 收敛速度：IPM, SQP > ALM > ADMM
  • ALM每次迭代的计算量较少，所以工程上很受欢迎