looyifan / Pluto

Created Wed, 02 Apr 2025 11:08:42 +0800 Modified Fri, 11 Apr 2025 15:48:56 +0800
4884 Words

PLUTO: Pushing the Limit of Imitation Learning-based Planning for Autonomous Driving

动机

  • 模型方法缺乏横向行为建模，导致不擅长横向任务
  • 模仿学习的局限性：
    • shortcut学习（只学到了递推自车历史状态完成规划）
    • 分布转移（训练集中所有数据都是居中行驶的，但是闭环测试中可能偏离车道，ego未学习到从偏离状态纠正到居中状态的能力）
    • 因果混淆

开创性思路

  • 基于查询的模型架构，anchor-based横向+anchor-free-based纵向
  • 提出了一种基于差分插值计算辅助损失的新方法
  • 提出了对比模仿学习框架，和新的数据增强方法，避免模型学到捷径或因果混淆

问题建模

  • \(N_{A}\)* 动态agents
  • \(N_{S}\)* 静态障碍物
  • 高精地图\(M\)
  • 其他交通环境信息（信号灯等）\(C\)
  • 历史观测时长\(T_{H}\)
  • 预测时长\(T_{F}\)

模块细节

pic

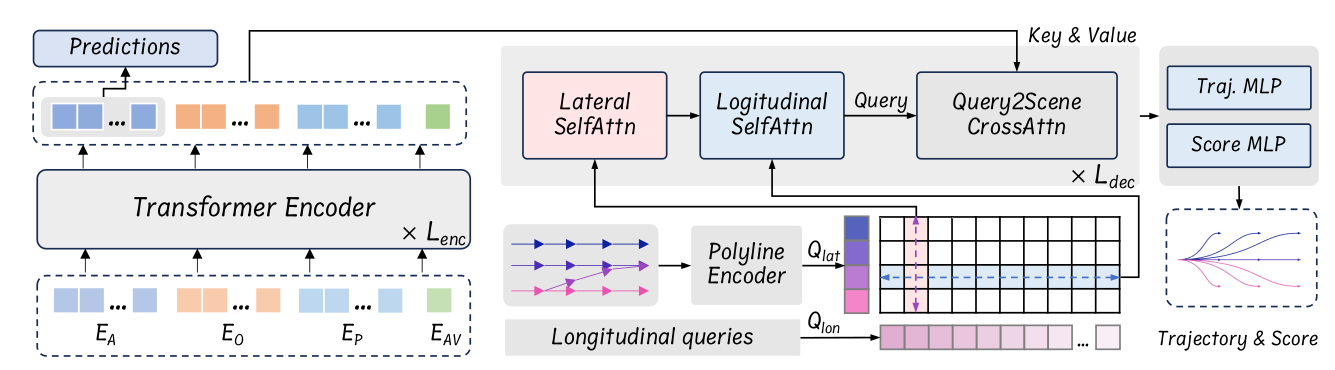
特征编码

Agent History Encoding

-\(t\)时刻障碍物的观测状态为\(s_{i}^{t}=(p_{i}^{t},\theta_{i}^{t},v_{i}^{t},b_{i}^{t},\Pi_{i}^{t})\)，其中\(p\)和\(\theta\)表示agent的位置和角度，\(v\)表示速度矢量，\(b\)表示长宽尺寸，\(\Pi\)是一个bool量，表示当前帧是否被观测到

  • 这里通过相邻两帧的状态量插值将历史状态序列转化为vector的形式，\(s_{i}^{t}=(p_{i}^{t}-p_{i}^{t-1},\theta_{i}^{t}-\theta_{i}^{t-1},v_{i}^{t}-v_{i}^{t-1},b_{i}^{t},\Pi_{i}^{t})\)，最终得到历史特征向量\(F_{A} \in R^{N_{A}*(T_{H}-1)*8}\)
  • 这里通过一个neighbor attention-based Feature Pyramid Network(FPN)对agent的历史信息进行提取，得到embedding\(E_{A} \in R^{N_{A}*D}\)

Static Obstacles Encoding

  • 静止障碍物的观测状态为\(o_{i}=(p_{i},\theta_{i},b_{i})\)，聚合得到\(F_{O} \in R^{N_{S}*5}\)
  • 通过一个两层的MLP进行提取得到embedding\(E_{O} \in R^{N_{S}*D}\)

AV’s State Encoding

  • 为了防止shortcuts学习，只输入ego当前帧的状态（位置、角度、速度、加速度和方向盘转角），为了避免生成的轨迹只是当前状态的简单外推，引入了attention-based state dropout encoder(SDE)进行编码，得到embedding\(E_{AV} \in R^{1*D}\)

Vectorized Map Encoding

  • 地图由\(N_{P}\)条polyline组成。
  • 我们对polyline上的每个点进行差分计算。第\(i\)个点的特征包括8个维度\((p_{i}-p_{0},p_{i}-p_{i-1},p_{i}-p_{i}^{left},p_{i}-p_{i}^{right})\)。其中 \(p_{0}\)表示polyline的第一个点\(p_{i}^{left}\)和\(p_{i}^{right}\)表示车道的左右边界点。
  • polyline的特征\(F_{P} \in R^{N_{p}*n_{p}*8}\)，\(n_{p}\)是每条polyline包含的点的数量。
  • 通过一个类PointNet网络提取embedding\(E_{p} \in R^{N_{p}*D}\)。

Scene Encoding

  • 由于前面的vector化过程，特征中只包含了相邻状态的差分信息，因此需要补充全局位置信息编码\(PE\)，这里是用的傅立叶位置编码。这里的全局位置点是取的动态agent当前（最新）帧的 \(p\)和 \(\theta\)，静态障碍物的 \(p\)和 \(\theta\)，地图元素polyline的第一个点。
  • 初始化了一个可学习的embedding \(E_{attr}\)用于编码每个对象的属性类别
  • 将各个来源的特征合并到一个tensor \(E_{0} = concat(E_{AV},E_{A},E_{O},E_{P})+PE+E_{attr} \in R^{(N_{A}+N_{S}+N_{P}+1)*D}\)
  • 随后通过 \(N\)层transform decoder进行特征提取
    • 第 \(i\)层的decoder步骤如下： $$E_{i-1}^{’}=LayerNorm(E_{i-1})$$ $$E_{i}=E_{i-1}+MHA(E_{i-1}^{’},E_{i-1}^{’},E_{i-1}^{’})$$ $$E_{i}=E_{i}+FFN(LayerNorm(E_{i}))$$
    • 其中MHA是标准的multi-head attention操作

多模态轨迹解码

  • 引入modality query生成多模态轨迹，根据之前的经验，anchor-free的learnable query会导致模态的坍塌和训练的不稳定，因此这里采用了semi-anchor based decoding结构，将横向和纵向解耦建模。

基于参考线的横向query

  • 通过DFS连接lane segment形成参考线，通过和Vectorized Map类似的编码过程得到lateral query \(Q_{lat} \in R^{N_{R}*D}\)，其中 \(N_{R}\)是参考线的数量

分解式横纵self attention

  • 纵向query是初始化了一个anchor-free learnable embedding \(Q_{lon} \in R^{N_{L}*D}\)

  • 合并 \(Q_{lat}\)和 \(Q_{lon}\)创建横纵联合query \(Q_{0}=Projection(concat(Q_{lat},Q_{lon})) \in R^{N_{R}*N_{L}*D}\)，上面的 \(Projection\)是一个简单的MLP

    • 将 \(Q_{lat}\)通过unsqueeze和repeat操作复制 \(N_{L}\)份，得到 \(Q_{lat}^{tmp}\in R^{N_{R}*N_{L}*D}\)
    • 将 \(Q_{lon}\)通过unsqueeze和repeat操作复制 \(N_{R}\)份，得到 \(Q_{lon}^{tmp}\in R^{N_{R}*N_{L}*D}\)
    • concat得到 \(Q^{tmp}\in R^{N_{R}*N_{L}*2D}\)
    • 最后MLP将 \(2D\)维度变成 \(D\)维

  • 这里如果直接对 \(Q_{0}\)进行global self attention，计算复杂度在 \(O(N_{R}^{2}N_{L}^{2})\)

  • 为了简化，先遍历 \(N_{L}\)维度，针对每个 \(N_{R}*D\)的query块计算self attention

    pic

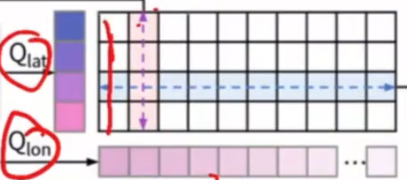
  • 再遍历\(N_{R}\)维度，针对每个\(N_{L}*D\)的query块计算self attention

    pic

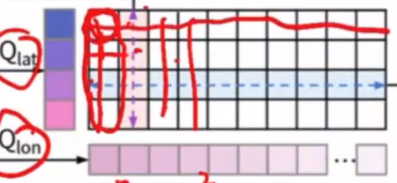
  • 最终的计算复杂度在 \(O(N_{R}^{2}N_{L}+N_{R}N_{L}^{2})\)

Query2Scene Cross Attention

  • 将上面得到的Query和Scene Encoding（作为key和value）进行Cross Attention

轨迹解码

  • 遍历 \(L_{dec}\)次self-attention和cross-attention操作: $$Q_{i-1}^{’}=SelfAttn(Q_{i-1},dim=0)$$ $$Q_{i-1}^{}=SelfAttn(Q_{i-1}^{’},dim=1)$$ $$Q_{i}=CrossAttn(Q_{i-1}^{},E_{enc},E_{enc})$$
  • 最终得到 \(Q_{dec}\)，通过两个MLP分别解码得到ego的未来轨迹和对应scores。其中每个轨迹点包含 \([p_{x},p_{y},cos\theta,sin\theta,v_{x},v_{y}]\) $$T_{0}=MLP(Q_{dec}),\pi_{0}=MLP(Q_{dec})$$
  • 此外，为了应对某些没有参考线的场景，用一个MLP直接解码\(E_{AV}\)得到一条轨迹 $$\tau^{free}=MLP(E^{’}_{AV})$$

Loss设计

Imitation Loss

  • 首先将GT轨迹的末状态投影到参考线上，找横向距离最近的参考线作为目标参考线。
  • 将目标参考线等分 \(N_{L}-1\)份，每一份对应上面 \(Q_{lon}\)的每个区域（格子）。包含GT状态投影的query被标记为目标query。
  • 通过将目标参考线和目标纵向query结合，得到目标监督轨迹 \(\hat{\tau}\)，通过 \(L1\)loss进行轨迹监督，通过corss-entropy loss进行score classification监督。 $$L_{reg}=L1_{smooth}(\hat{\tau},\tau^{gt})+L1_{smooth}(\tau^{free},\tau^{gt})$$ $$L_{cls}=CrossEntropy(\pi_{0},\pi_{0}^{*})$$
    • 其中， \(\pi_{0}^{*}\)是根据 \(\hat{\tau}\)的编号计算得到的one-hot编码
  • 最终的Imitation Loss是上面两个loss的加和 $$L_{i}=L_{reg}+L_{cls}$$

Prediction Loss

  • 针对每个动态agent，通过一个简单的双层MLP生成单一模态的预测轨迹 $$P_{1:N_{A}}=MLP(E_{A}^{’})$$
  • 预测loss设计如下： $$L_{p}=L1_{smooth}(P_{1:N_{A}},P_{1:N_{A}}^{gt})$$

Efficient Differentiable Auxiliary Loss

  • 根据过往经验，单纯靠模仿学习不足以杜绝不合理的规划结果，例如与静止障碍物碰撞或偏离可行驶路径等现象。因此，在训练阶段，将这些约束作为辅助loss至关重要。
  • 问题的关键在于如何将这些约束设计成可导的形式，使其可以端到端的进行训练。常用的手段是一种叫做可微分光栅化的技术。
    • 使用可微核函数将每个轨迹点转换为光栅化图像。
    • 使用图像空间内的障碍物掩模计算损失。
  • 但是该方法对计算量和内存的要求都比较大，限制较多。因此本文提出了一种基于differentiable interpolation的新方法。本文以可行驶区域约束为例来阐明该方法。

Cost Map Construction

  • 第一步是将约束转换为一个queryable cost-map。对于可行驶区域约束来说，利用Euclidean Signed Distance Field (ESDF)进行cost表征。此过程包括将不可驾驶区域（例如路外区域）映射到H×W大小的栅格化二值mask上。
  • 与现有方法相比，该方法的一个显著优势是它不需要将轨迹渲染成一系列图像，从而显著降低了计算需求。

Loss Calculation

pic

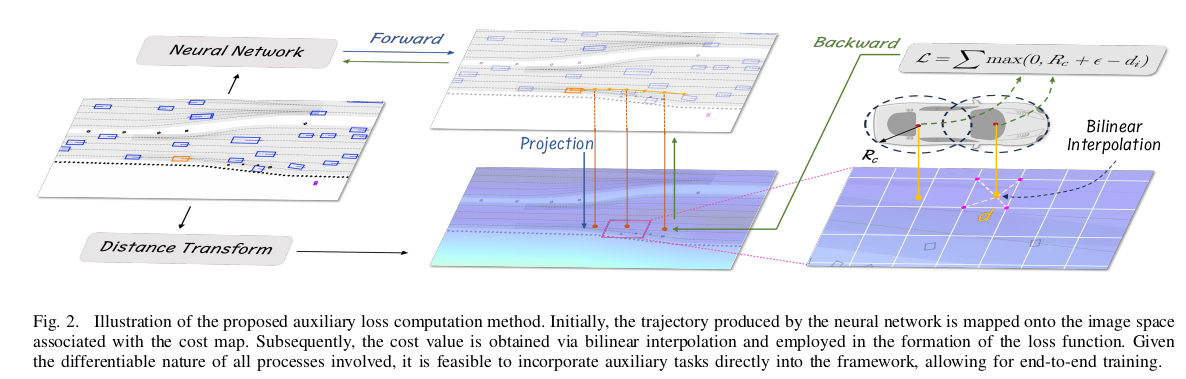
  • 用 \(N_{C}\)个覆盖ego的圆进行建模，ego轨迹点决定了这些圆的中心，这些圆可以用可微分的方式推导出来。
  • 对于与轨迹点关联的每个覆盖圆 \(i\)，我们通过投影和双线性插值得到其有符号距离值 \(d_{i}\)。为了确保ego遵守可行驶区域约束，当 \(d_{i}\)低于圆的半径 \(R_{c}\)时，我们对模型施加惩罚： $$L_{aux}=\frac{1}{T_{f}}\sum_{t=1}^{T_{f}}{\sum_{i=1}^{N_{c}}{max(0,R_{c}+\epsilon-d_{i}^{t})}}$$
    • 其中 \(\epsilon\)是安全阈值

Contrastive Imitation Learning Framework

  • 为了解决分布转移和因果混淆问题
  • 步骤：
    • 假设当前有一个数据样本 \(x\)，通过一个positive data augmentation模块 \(\Gamma^{+}\)和一个negative data augmentation模块 \(\Gamma^{-}\)分别生成一个正样本 \(x^{+}\)和负样本 \(x^{-}\)。
    • 前面的Scene Encoding部分会将样本 \(x\)编码为隐式特征 \(h(\cdot)\)。这里将原始样本、正负样本的隐式编码通过一个两层的MLP分别映射到一个新的空间，表征为 \(z,z^{+},z^{-}\)。
    • 利用一个triplet contrastive loss来增强 \(z\)和 \(z^{+}\)的相似度，降低 \(z\)和 \(z^{-}\)的相似度。
    • 最后将样本 \(x\)和 \(x^{+}\)的解码轨迹用于imitation loss和auxiliary loss的计算
  • 在实际操作中，我们随机采样 \(N_{bs}\)个样本，每个样本都过一遍positive和negative augmentation，从而得到 \(3N_{bs}\)个样本。
  • 每个样本都过一遍encoder和projection head。softmax-based triple contrastive loss公式如下： $$L_{c}=-log\frac{exp(sim(z,z^{+})/\sigma)}{exp(sim(z,z^{+})/\sigma) + exp(sim(z,z^{-})/\sigma)}$$ $$sim(u,v)=u^{T}v/\lVert u \rVert \lVert v \rVert$$
    • \(\sigma\)表示温度参数（temperature parameter）
  • 注意，原始样本和正样本都利用未改动过的GT进行监督训练（ \(L_{i}, L_{p},L_{aux},L_{c}\)），但是负样本只用于contrastive loss（ \(L_{c}\)）的计算。因为在负样本中，原始的GT可能已经是无效的了。

Data augmentations

  • 数据增强是对比学习发挥作用的关键。虽然基于扰动的增强很普遍，但替代增强策略的探索仍然不足。在此背景下，本文提出了六个精心设计的增强函数，用于定义对比任务。
  • State Perturbation \(\in \Gamma^{+}\)
    • 对自动驾驶汽车的当前位置、速度、加速度和转向角引入轻微的随机干扰。这种增强旨在使模型能够学习与训练分布略有偏差的恢复策略。
  • Non-interactive Agents Dropout \(\in \Gamma^{+}\)
    • 从输入场景中忽略不与ego交互的agent。判断agent与ego是否有交互是通过其未来bounding box与ego轨迹的交点来识别的。这种增强可以防止模型通过模仿非交互agent来学习行为，从而鼓励模型辨别与有交互关系的agent的真正因果关系。
  • Leading Agents Dropout \(\in \Gamma^{-}\)
    • 删除位于ego前面的所有leading agent。这种增强训练了模型的跟驰前车行为，以防止追尾碰撞。
  • Leading Agent Insertions \(\in \Gamma^{-}\)
    • 在ego未来会运动的路线上插入一个agent，使得ego如果按照GT走的话会发生碰撞。插入的车辆的轨迹数据来自当前小批量中随机选择的agent，以保持数据的真实性。
  • Interactive Agent Dropout \(\in \Gamma^{-}\)
    • 删除与ego有直接或间接交互的agent。该功能旨在训练模型在复杂场景中与不太直观的交互agent之间的交互行为，如无保护的左转和变道场景。
  • Traffic Light Inversion \(\in \Gamma^{-}\)
    • 在ego接近由交通灯控制的十字路口而没有前方车辆的情况下，人为反转交通灯状态（例如，从红色变为绿色）。用于教导模型遵守基本的交通灯规则。

Total Loss

$$L=w_{1}L_{i}+w_{2}L_{p}+w_{3}L_{aux}+w_{4}L_{c}$$

后处理

  • 前面的轨迹解码器模块会输出多模态的自车规划轨迹 \(T_{0} \in R^{N_{R}N_{L}*T_{F}*6}\)和对应score \(\pi_{0} \in R^{N_{R}N_{L}}\)
  • 为了计算复杂度满足要求，先根据scores从前面的轨迹中选出top K
  • 遍历K条轨迹，根据ego状态，利用一个LQR的优化器计算出跟踪轨迹的控制量，再用自行车模型积分控制量得到一条更精细的轨迹
  • 对精细轨迹进行rule-based评估（引入其他agent的预测信息），评估项包括驾驶进度、舒适度、交规、碰撞
  • 最后将规则得分和网络预测得分加权求和，排序得到最优轨迹

实验结果

  • 与其他方法的对比实验

pic

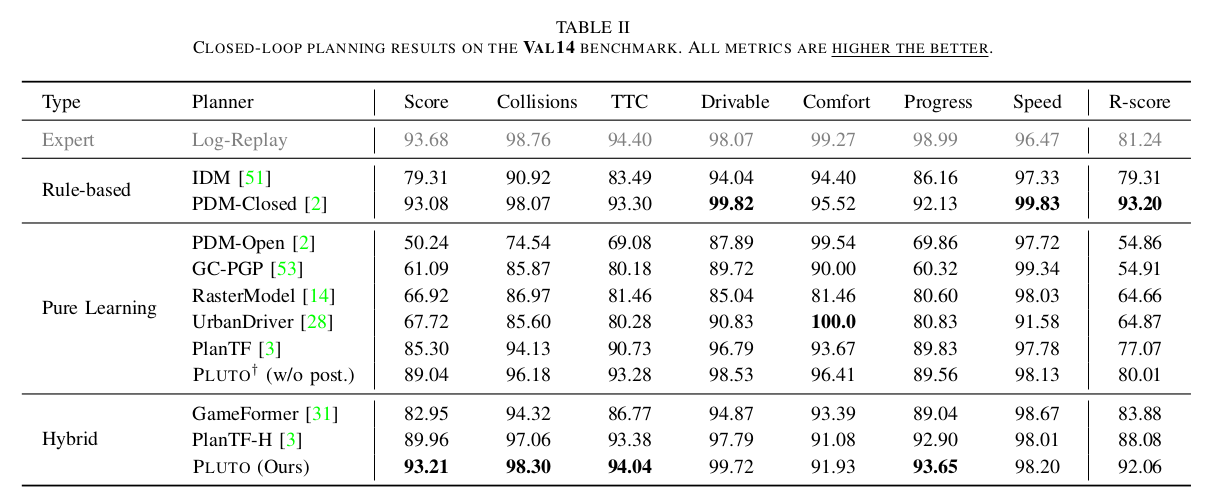
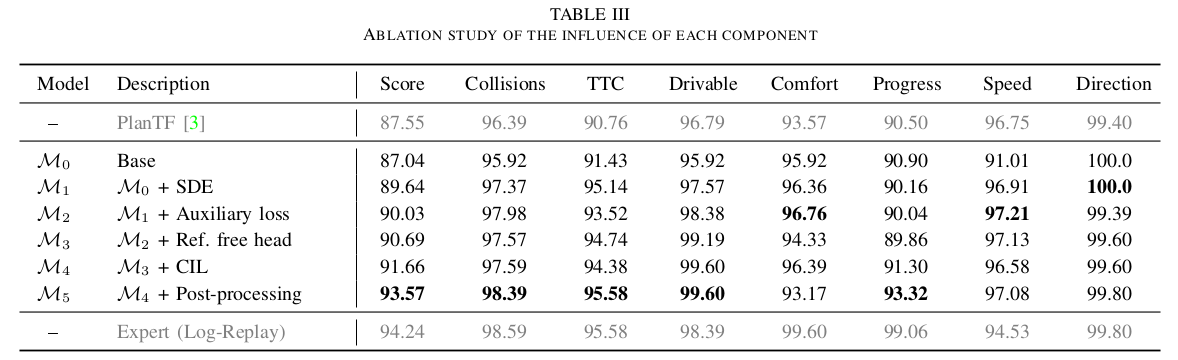
  • 消融实验

pic