GoalFlow: Goal-Driven Flow Matching for Multimodal Trajectories Generation in End-to-End Autonomous Driving

贡献

设计了一种创新的目标点确立方法，通过实验验证了其在引导生成模型进行轨迹生成方面的有效性。
我们将flow matching技术首次引入端到端自动驾驶系统，实现了与目标点引导机制的无缝融合。
开发了基于影子轨迹的创新轨迹选择机制，通过虚拟轨迹分析有效缓解潜在目标点偏差问题。
在Navsim仿真平台上，本方法取得了当前最优的测试结果。

方案

预备知识

相较于扩散模型专注于学习逐步逆向消除时序叠加噪声以恢复数据，flow matching着力于学习数据分布间的可逆映射变换。设$\pi_{0}$表示简单分布（通常为标准正态分布$p(x)=N(x|0,I)$），$\pi_{1}$表示目标分布。设$x_{0}$采样自$\pi_{0}$分布，$x_{1}$采样自$\pi_{1}$分布，时间参数$t\in\lbrack0,1\rbrack$。定义$x_{0}$到$x_{1}$的传输路径为直线形式，即中间状态$x_{t}=(1−t)x_{0}+tx_{1}$，其演化方向始终由$x_{1}−x_{0}$确定。通过构建神经网络$v_{\theta}$基于当前状态$x_{t}$与时序参数$t$预测方向量$x_{1}−x_{0}$，可优化$v_{\theta}(x_{t},t)$与$x_{1}−x_{0}$间的损失函数，从而获得从初始分布$\pi_{0}$到目标分布$\pi_{1}$的传输路径。
在此框架下，rectified flow(Flow straight and fast: Learning to generate and transfer data with rectified flow)通过最优传输位移量构建路径，该方法兼具简洁性与高效性。

概述

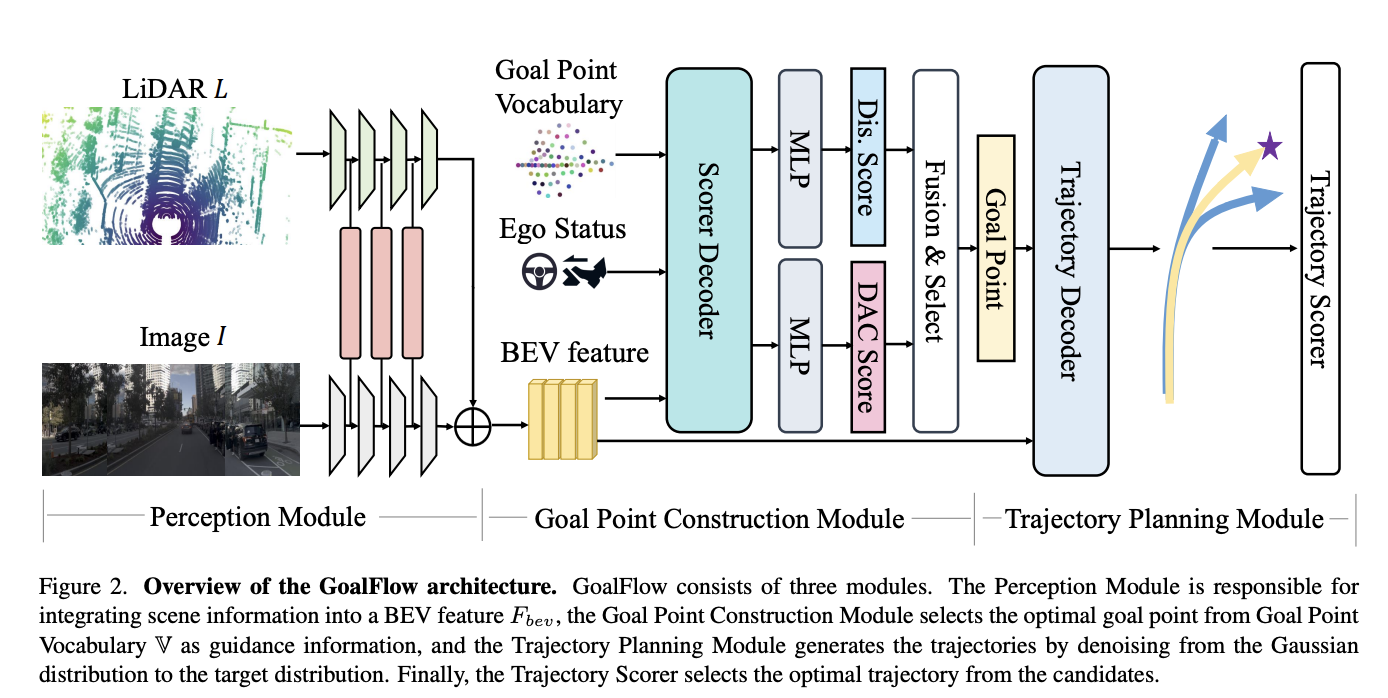
GoalFlow整体架构包含三个核心模块：在感知模块中，通过融合摄像头图像$I$与激光雷达点云$L$，提取蕴含环境信息的BEV特征$F_{bev}$；目标点构建模块专注于生成精确的轨迹引导信息，通过构建目标点词典并采用评分$V=\lbrace g_{i}\rbrace^{N}$机制筛选最优目标点$g$；轨迹规划模块首先生成多模态轨迹集合$T=\lbrace \hat{\tau_{i}} \rbrace^{M}$，随后通过轨迹评分机制确定最优轨迹$\tau$。

感知模块

在第一步多模态数据融合中，我们融合图像与激光雷达数据生成BEV特征$F_{bev}$以捕获丰富的道路信息。单一传感器存在信息缺失问题：例如激光雷达无法获取交通灯状态，而摄像头难以精确定位物体。
本工作采用Transfuser架构实现模态融合。前视、左视、右视摄像头视角拼接为单张图像$I\in R^{3\times H_{1}\times W_{1}}$，激光雷达点云数据构建为张量$L\in R^{K\times 3}$。两类数据经过独立主干网络提取特征后，通过多级Transformer模块进行跨模态特征融合，最终生成全面表征场景的BEV特征$F_{bev}$。为确保自车与周边物体及地图信息的有效交互，我们基于高精地图与边界框提供的损失函数对BEV特征实施辅助监督。

目标点构建模块

在本模块中，我们通过构建精确目标点为轨迹生成过程提供引导。无约束的基于扩散方法常导致轨迹过度发散，增加轨迹选择复杂度。我们的核心发现在于：目标点包含对短期未来位置的精准描述，可为生成模型施加强约束。因此，将传统规划模块拆分为两步执行：首先构建精确目标点，其次通过规划生成轨迹。
目标点库：受VADv2启发，我们通过对轨迹终点空间进行离散化构建候选目标点集，实现不依赖高精地图的解决方案。具体而言，在训练数据中对轨迹端点$p_{i}=(x_{i},y_{i},\theta_{i})$进行聚类得到$N$个聚类中心，形成目标点词典$V$。为确保词典能表征细粒度的空间位置，通常将$N$设置为较大数值（4096或8192）。

目标点选择模块

高质量轨迹通常具备以下特征：与真实轨迹距离接近且位于可行驶区域内。为此，我们通过距离评分$\hat{\delta}^{dis}$与可行驶区域合规评分$\hat{\delta}^{dac}$对目标点词典$V$中的每个候选点$g_{i}$进行双重评估。距离评分衡量目标点$g_{i}$与真实轨迹终点$g^{gt}$的接近程度，采用连续值表示，取值范围$\hat{\delta}^{dis}\in\lbrack0,1\rbrack$，数值越大表示与$g^{gt}$越接近；可行驶区域合规评分确保目标点位于合法驾驶区域，采用二元值$\hat{\delta}^{dac}\in\lbrace 0,1\rbrace$，1表示目标点符合可行驶区域要求，0则表示处于非驾驶区域。
为构建目标距离评分$\hat{\delta_{i}}^{dis}$，我们采用softmax函数将目标点$g_{i}$与真实目标点$g^{gt}$之间的欧氏距离映射至$\lbrack0,1\rbrack$区间：

$$\hat{\delta_{i}}^{dis}=\frac{exp(-\Vert g_{i}-g^{gt}\Vert_{2})}{\sum_{j} exp(-\Vert g_{j}-g^{gt}\Vert_{2})}$$

针对可行驶区域合规评分$\hat{\delta_{i}}^{dac}$的构建，我们引入影子车辆概念——其边界框根据目标点$g_{i}$的位置与航向角$(x_{i},y_{i},\theta_{i})$以及自车几何参数确定。设$\lbrace p^{j}\rbrace^{4}$表示影子车辆四个角点的位置集合，$DA $为表征可行驶区域的多边形区域，则合规评分定义为：

$$\hat{\delta_{i}}^{dac}=\begin{cases} 1 &\text{if } \forall j,p^{j} \in DA \ 0 &\text{if } otherwise \end{cases}$$

我们通过综合$\hat{\delta_{i}}^{dis}$与$\hat{\delta_{i}}^{dac}$计算最终评分，选取最终评分最高的目标点作为轨迹生成依据。

$$\hat{\delta_{i}}^{final}=w_{1}log\hat{\delta_{i}}^{dis}+w_{2}log\hat{\delta_{i}}^{dac}$$

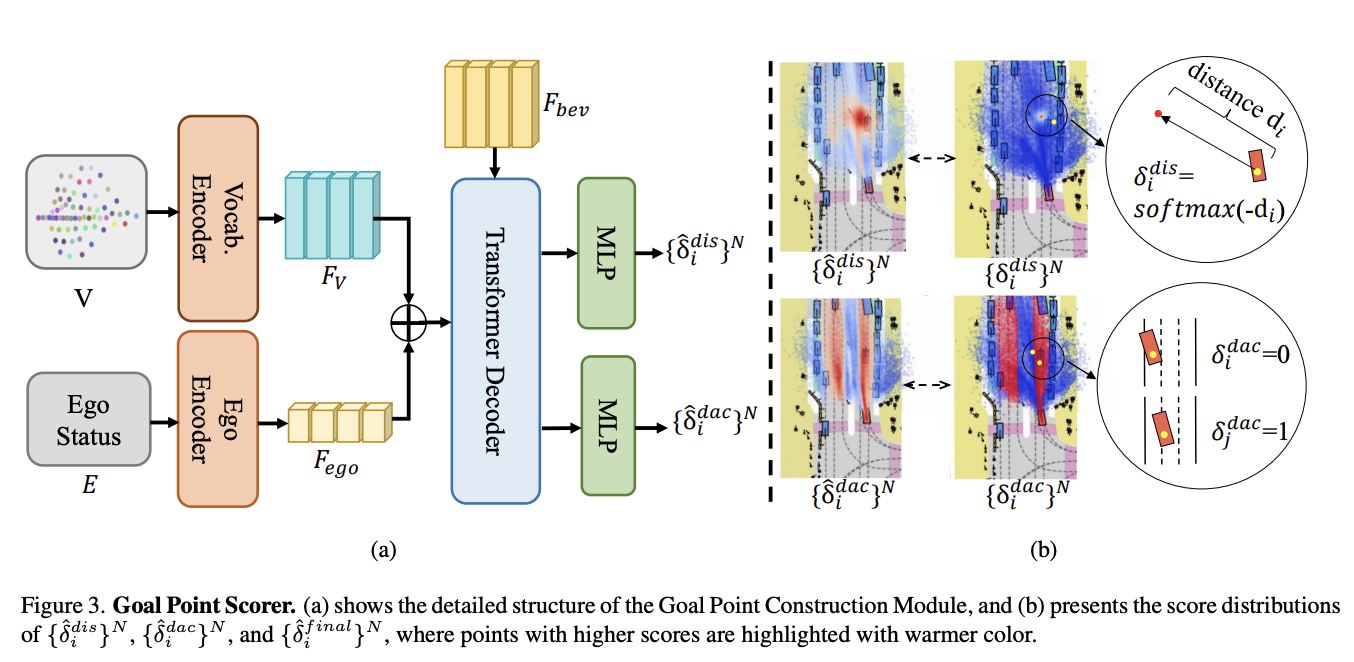
如图3(a)所示，基于Transformer的评分解码器以特征向量$F_{v}$与$F_{ego}$的加和结果作为查询向量，BEV特征$F_{bev}$作为键/值向量。解码输出经两个独立的多层感知机(MLP)处理后，为词典$V$中各候选点生成$\hat{\delta}^{dis}$与$\hat{\delta}^{dac}$评分。图3(b)展示了双评分分布可视化结果，其中暖色调点表示更高评分。实验观测表明：$\hat{\delta}^{dis}$有效指示期望未来位置，而$\hat{\delta}^{dac}$可精准识别目标点是否位于可行驶区域

轨迹规划模块

在轨迹规划模块中，我们通过生成模型产生受约束的高质量轨迹候选集，并基于评分机制筛选最优轨迹。基于扩散方法的生成模型如DDPM和DDIM通常需要复杂的去噪路径，导致推理阶段产生显著时间开销，难以满足自动驾驶等实时系统的需求。相比之下，基于flow matching中最优传输路径的rectified flow仅需少量推理步骤即可获得理想结果。本工作采用rectified flow作为生成模型，以BEV特征$F_{bev}$与目标点$g$为条件，生成多模态轨迹集合。
我们通过建模从噪声分布到目标轨迹分布的迁移过程生成多模态轨迹。在此分布迁移过程中，给定当前状态$x_{t}$及时序参数$t$预测轨迹偏移量$v_{t}$。

$$v_{t}=\tau^{norm}-x_{0}$$

$$x_{t} = (1-t)x_{0}+t\tau^{norm}$$

$$\tau^{norm} = \cal H(\tau^{gt})$$

其中$\tau^{gt}$是轨迹GT，$\tau^{norm}$是它的归一化形式。定义$\cal H(\cdot)$为轨迹归一化运算。$x_{0}$变量表征噪声分布，服从$x_{0}\thicksim N(0,\sigma^{2}I)$。通过$x_{0}$与$\tau^{norm}$的线性插值获得中间状态$x_{t}$。
如图4所示，通过级联编码器提取多维度特征：$x_{t}$经线性层编码，时序参数$t$与目标点通过正弦编码转化为特征向量，BEV特征$F_{bev}$与自车特征$F_{ego}$经环境编码器融合获得环境特征$F_{env}$。

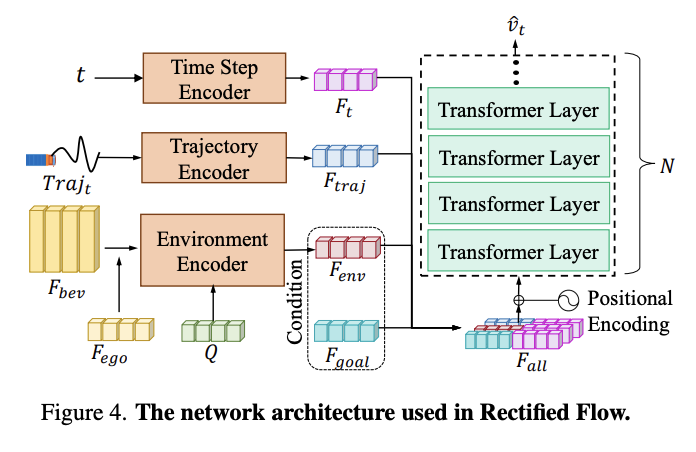
$$F_{env}=E_{env}(Q,(F_{BEV}+F_{ego}),(F_{BEV}+F_{ego}))$$

其中，$E_{env}$指基于Transformer架构的编码器，$ Q$表示可学习嵌入向量，$F_{ego}$表征自车状态特征，其中编码了自车的运动学信息（如速度、加速度等）。
通过将环境特征$F_{env}$、目标点特征$F_{goal}$、轨迹特征$F_{traj}$及时序特征$F_{t}$进行特征拼接，形成综合特征$F_{all}$——该特征集成当前状态、时序信息及场景上下文。组合特征随后输入多层注意力网络，最终预测分布迁移量$v_{t}$。

$$\hat{v_{t}}=\cal G(F_{all},F_{all},F_{all})$$

$$F_{all} = Concat(F_{env}, F_{goal}, F_{traj}, F_{t})$$

其中，网络$\cal G$由$N$层注意力模块构成。我们基于噪声分布$x_{0}$与预测迁移量$\hat{v_{t}}$重构轨迹分布。具体而言，通过修正流执行多次推理步骤，逐步将噪声分布$x_{0}$转换为目标分布$\tau^{norm}$，最终对$\tau^{norm}$实施去归一化处理得到最终轨迹$\hat{\tau}$

$$\hat{\tau} = \cal H^{-1}(\hat{\tau}^{norm})$$

$$\hat{\tau}^{norm}=x_{0}+\frac{1}{n}\sum_{i}^n\hat{v} _{t _{i}}$$

式中，$n$表示总推理步数，$t_{i}$为第$i$步采样的时间步参数，满足$t_{i}\in\lbrack0,1\rbrack$。$\cal H^{-1}(\cdot)$表示去归一化运算，将归一化轨迹恢复至实际物理尺度。
在轨迹选择环节，SparseDrive与Diffusion-ES等方法需对生成轨迹进行运动学仿真，预测其与周边交通参与者的潜在碰撞风险以筛选最优轨迹，该过程显著增加推理耗时。本方法通过目标点引导实现轨迹选择的流程简化：综合考虑轨迹与目标点的距离偏差及自车行驶进度，借助轨迹评分器完成最优轨迹选择。TODO：没有显示碰撞检测了，只关注导航进度和轨迹终点约束，真的能选出合理的轨迹吗?

$$f(\hat{x} _{i})=-\lambda _{1}\Phi(f _{dis}(\hat{\tau} _{i}))+\lambda _{2}\Phi(f _{pg}(\hat{\tau} _{i}))$$

式中，$\Phi(\cdot)$表示极小极大运算。$f_{dis}( \hat{\tau_{i}} )$计算轨迹$\hat{\tau_{i}}$与目标点$g$的$L2$距离偏差，$f_{pg}(\hat{\tau_{i}})$评估轨迹$\hat{\tau_{i}}$形势进度的$L_{2}$距离指标。
此外，预测目标点可能存在偏差误导轨迹生成。为此，我们在生成阶段对目标点进行屏蔽处理，构建影子轨迹。若影子轨迹与主轨迹呈现显著偏离，则判定该目标点不可靠，转而采用影子轨迹作为最终输出。影子轨迹应该就是没有goal引导的情况下得到的一条fallback轨迹

训练Loss

首先，我们专门优化感知特征提取器，施加多感知监督损失，包括高精地图交叉熵损失$L_{HD}$、3D边界框分类损失$L_{bbox}$以及边界框位置回归的$L_{1}$损失$L_{loc}$。该阶段旨在通过多感知监督增强BEV特征的信息表征能力。具体损失函数定义如下：

$$L_{perception}=w_{1}L_{HD}+w_{2}L_{bbox}+w_{3}L_{loc}$$

其中，$w_{1}=10,w_{2}=1,w_{3}=10$。对目标生成器的distance score($L_{dis}$) 和 DAC score($L_{Ldac}$)采用cross entropy loss，$w_{4}=1,w_{5}=0.005$。

$$L_{goal} = w_{4} L_{dis} + w_{5} L_{dac}$$

$$L_{dis}=-\sum_{i=i}^{N} \delta_{i}^{dis}log(\hat{\delta}_{i}^{dis})$$

$$L_{dac} = −\delta^{dac}log\hat{\delta}^{dac}−(1−\delta^{dac})log(1−\hat{\delta}^{dac})$$

对多模态规划器施加$L_{1}$loss

$$L_{planner} = \vert v_{t} − \hat{v}_{t}\vert$$

实验

数据集

本实验在Openscene数据集完成验证。该数据集包含120小时自动驾驶数据，其端到端仿真环境Navsim采用1192个训练验证场景与136个测试场景，共计超10万样本（采样频率2Hz）。每个样本包含：8个视角的摄像头图像、5个激光雷达的融合点云、自车状态信息以及高精地图与目标物的标注信息。

评价指标

在Navsim仿真环境中，生成的2Hz、4秒时长的初始轨迹通过LQR控制器进行插值处理，得到10Hz、4秒时长的平滑轨迹。通过以下闭环指标对轨迹进行综合评分：无责任碰撞率($S_{NC}$)、可行驶区域合规率($S_{DAC}$)、带边界约束的碰撞时间($S_{TTC}$)、自车行驶进度($S_{EP}$)、舒适性指数($S_{CF}$)及行驶方向合规率($S_{DDC}$)。最终评分通过加权聚合上述指标获得。由于实际约束条件限制，$S_{DDC}$指标未纳入最终评分计算。

$$S_{PDM}=S_{NC}\times S_{DAC}\times S_{TTC}\times (\frac{5\times S_{EP} + 5 \times S_{CF} + 2\times S_{DDC} }{12})$$

基线算法

恒定速度模型(Constant Velocity)：假设自车保持当前速度匀速前进
自车状态MLP(Ego Status MLP)：仅以自车当前状态为输入，通过多层感知机生成轨迹
PDM-Closed：以真实感知为输入，通过基于规则的IDM方法生成多条轨迹，并由PDM评分器筛选最优轨迹
Transfuser：融合摄像头与激光雷达输入，通过Transformer生成BEV特征用于轨迹生成
LTF：Transfuser的轻量版本，将激光雷达主干网络替换为可学习嵌入向量，在NavSim中取得与Transfuser相近效果
UniAD：采用多组Transformer架构差异化处理信息，通过查询机制实现规划专用信息传递
PARA-Drive：基于BEV特征并行执行地图构建、路径规划、运动预测及占用预测任务，相较UniAD实现方案创新

模型参数设置

rectified flow的训练遵循无分类器引导范式，通过在条件集中随机掩码特征以增强模型鲁棒性。训练阶段使用真实轨迹的终点指导流匹配过程，测试阶段则通过目标点词典中筛选最高评分点确定轨迹生成目标。采样过程采用非线性重缩放时间步长平滑方法（替代均匀间隔采样）。每次推理生成128/256条候选轨迹，经轨迹评分器筛选确定最优解。所有实验均在4个计算节点上完成，每个节点配置8块RTX 4090或RTX 3090显卡。

实验结果

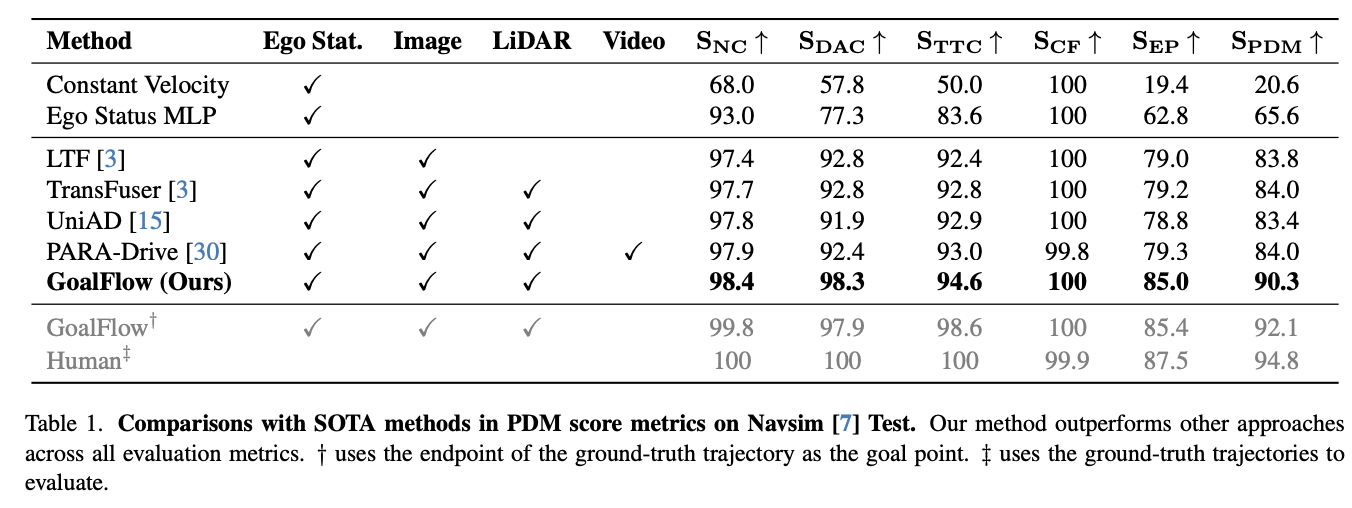
如表1所示，我们将本方法与当前端到端自动驾驶领域多种前沿算法进行对比（最优指标以加粗显示）。Navsim环境测试表明，GoalFlow在综合评分上持续超越其他方法。具体而言，本方法在可行驶区域合规率(DAC)指标上较次优方法提升5.5分，自车行驶进度(EP)指标提升5.7分，证明GoalFlow对车辆行驶区域的约束力更强，有效提升系统安全性。此外，本方法在保障安全的前提下实现了更高的行驶速度。补充实验中，将预测目标点替换为真实轨迹终点时，评分达到92.1分（接近人类驾驶轨迹的94.8分），显著验证目标点在自动驾驶中的强引导能力。

消融实验：
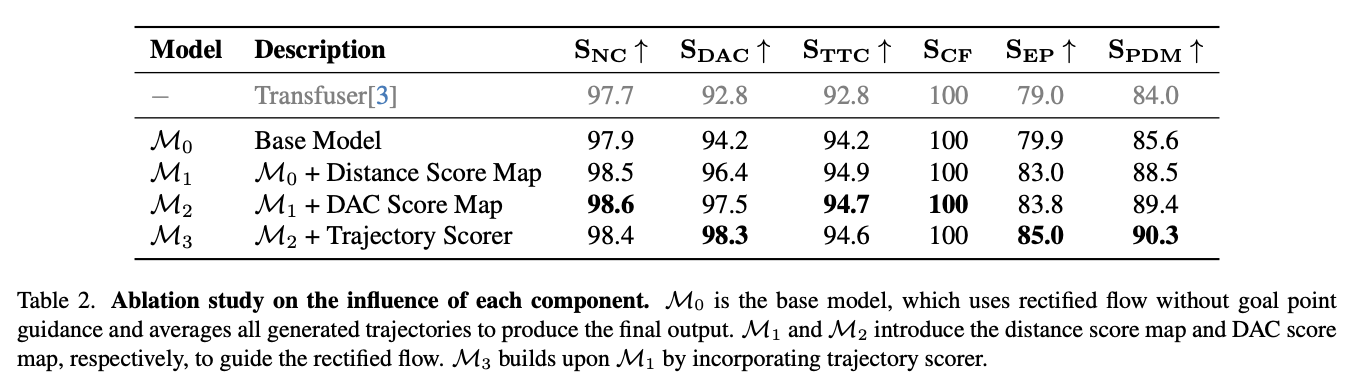
- 如表2所示，我们通过消融实验验证各组件对系统性能的影响。其中，M0表示仅采用修正流生成轨迹的基础模型。实验结果显示，M0在Navsim平台上持续超越基线方法，尤其在可行驶区域合规率(DAC)与碰撞时间(TTC)指标表现突出，表明基于流匹配的基础模型有效学习了与地图信息及周边交通参与者的交互规律，验证了流模型自身具备强大的场景建模能力。
- M1在M0基础上引入距离评分分布建模，筛选最高分目标点指导修正流。实验显示该方法带来最显著的性能提升，证实了将轨迹规划任务解耦为"目标点预测→目标点引导轨迹生成"两阶段策略的有效性。具体而言，通过将复杂任务分解为两个更简单的子任务（目标点预测与目标点引导轨迹生成），系统性能获得显著优化。
- M2在M1基础上增加可行驶区域合规评分(DAC)分布预测。主要改进体现在DAC指标上，通过引入多视角评估器，模型得益于更鲁棒的评估体系，从而提升整体表现。
- M3进一步整合包含轨迹选择与目标点验证机制的轨迹评分器，使GoalFlow系统可靠性得到全面提升。

推理步骤影响分析
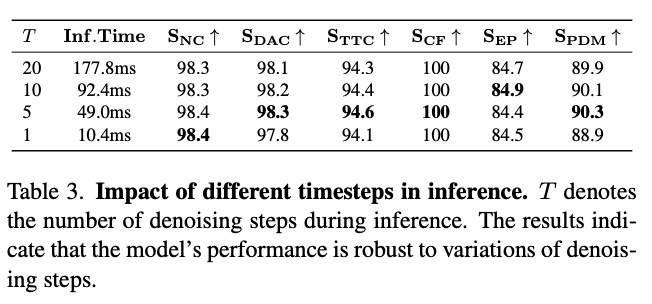
- 如表3所示，我们测试了不同去噪步数对系统性能的影响。实验表明：当推理步数从20步递减至1步时，各项评分保持稳定。值得注意的是，即使仅执行单步推理，系统仍能保持优异性能。这凸显了流匹配相较扩散模型的优势——流匹配采用直线型传输路径，在推理阶段仅需少量步骤即可完成噪声分布到目标分布的迁移。当推理步数从20步减至1步时，单样本去噪时间降至原始时间的6%，这种高效推理特性对实时性要求严苛的自动驾驶系统至关重要。

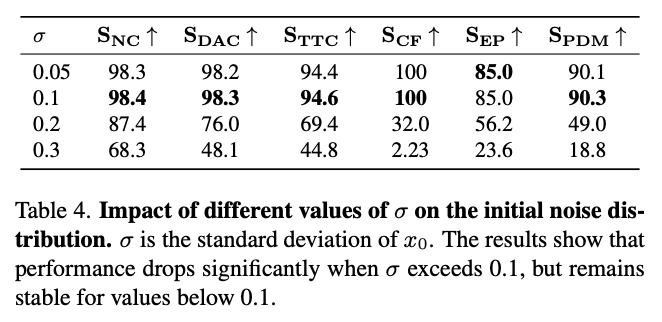
初始噪声影响研究
- 实验中，初始噪声服从高斯分布$N(0,\sigma^{2}I)$。如表4所示，我们探究了噪声方差对轨迹生成的影响。结果表明：噪声设置对评分具有显著影响。当噪声方差过高（$\sigma=0.3$时），生成轨迹呈现过度抖动特性，舒适度评分骤降至2.23，表明轨迹形态失去连贯性；反之，当噪声方差过低时，流匹配易退化为回归模型，导致可供筛选的轨迹多样性降低，进而影响整体评分表现。

looyifan / GoalFlow