GenAD: Generative End-to-End Autonomous Driving
方案细节
Instance-Centric Scene Representation
Image to BEV
-
初始化一个 \(H\times W\)的BEV query \(B_{0}\),将摄像头提取的multi-scaled feature \(F\)与之进行deformable cross-attention,得到BEV feature
$$B=DA(B_{0},F,F)$$
- \(DA(Q,K,V)\)表示deformable cross-attention
BEV to Map
-
借鉴VAD的思路,初始化一个learnable query \(M_{0}\),集合BEV feature通过global cross-attention得到地图元素表达 \(M\)
$$M=CA(M_{0},B,B)$$
BEV to agent
-
类似地图元素,agent特征的提取方式为:
$$A=DA(A_{0},B,B)$$
- \(A_{0}\)是learnable query
- 这边得到agent特征后,会接一个3D目标检测head进行agent的位置、朝向、种类的解码
Instance-centric scene representation
- 将上面学到的agent特征和ego query拼在一起, \(I=concat(e,A)\)
- 学习agent和ego之间的相互影响, \(I=SA(I,I,I)\), \(SA(Q,K,V)\)表示self-attention
- 学习agent、ego和地图之间的交互, \(I=CA(I,M,M)\)
Trajectory Prior Modeling
-
自车和障碍物的轨迹都是高度结构化的(连续的),并遵循一定的模式。例如,当车辆以恒定速度行驶时,大多数轨迹都是直线,当车辆右转或左转时,其中一些轨迹是曲率接近恒定的曲线。只有在极少数情况下,轨迹才会是曲折的。考虑到这一点,我们采用变分自动编码器(VAE)架构来学习latent spaec \(Z\),以此来建模trajectory prior。
-
这里利用一个GT轨迹encoder \(e_{f}\)来建模 \(p(z|\mathsf{\mathbf{T}}(T,f))\),它将未来轨迹映射到latent spaec \(Z\)。encoder \(e_{f}\)输出一组 \(\mu_{f}\)和 \(\sigma_{f}\)来表示GMM的均值和方差。
-
\(e_{f}\)代码实现
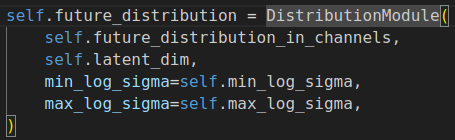
$$p(z|\mathsf{\mathbf{T}}(T,f)) \thicksim N(\mu_{f},\sigma_{f})$$
-
-
分布 \(p(z|\mathsf{\mathbf{T}}(T,f))\)包含未来轨迹的先验,可用于提高障碍物和自车的运动预测和规划的真实性。
Latent Future Trajectory Generation
-
有了未来轨迹的latent distribution作为先验后,我们需要将未来轨迹从latent spaec \(Z\)中解码出来。最直接的办法是用一个MLP在BEV space下解码出轨迹点,但是这种方法无法模拟障碍物和自车随时间变化产生的交互。为了建模每个实例在不同时间戳之间的时间上的联系,对联合概率分布 \(p(\mathsf{\mathbf{T}}(T,f)|z)\)进行分解:
$$p(\mathsf{\mathbf{T}}(T,f)|z)=p(w^{T+1}|z^{T})\cdot p(w^{T+2}|w^{T+1},z^{T})…p(w^{T+f}|w^{T+1},…,w^{T+f-1},z^{T})$$
-
我们从分布 \(N(\mu_{f},\sigma_{f})\)中采样一组 \(\mu_{f}\)和\(\sigma_{f}\)作为当前时刻的 \(z^{T}\)的latent state。不同于其他方法中一次性将轨迹decode出来,这边是采用分步解码的方法。引入decoder \(d_{w}\)(MLP)从latent state中解码轨迹点。 \(p(w^{T+1}|z^{T})\)通过 \(w=d_{w}(z)\)来表示。
- 采样代码实现:
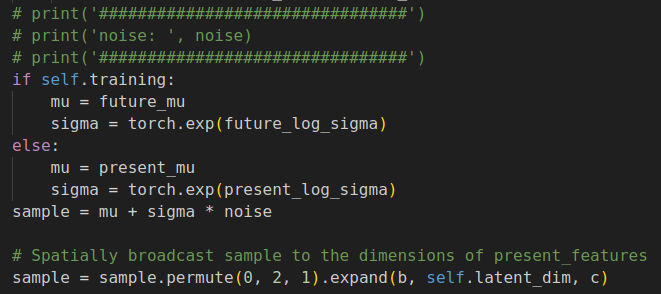
- 采样代码实现:
-
我们通过GRU模型来建模状态随时间的演化。 \(z^{T+1}=g(z^{T})\),然后再解码下个时刻的轨迹点, \(w^{T+1}=g(z^{T+1})\), \(T+f\)时刻同理。
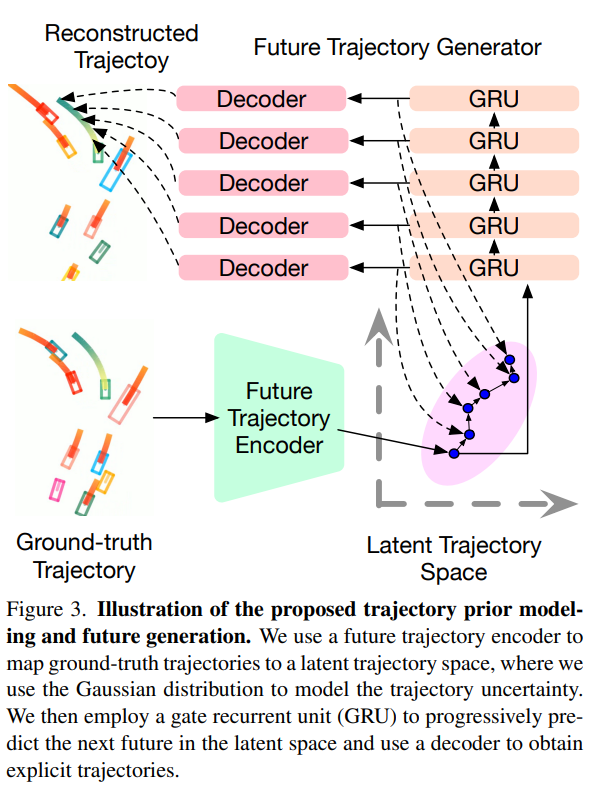
-
从distribution里面采样出的latent state进行future state的预测
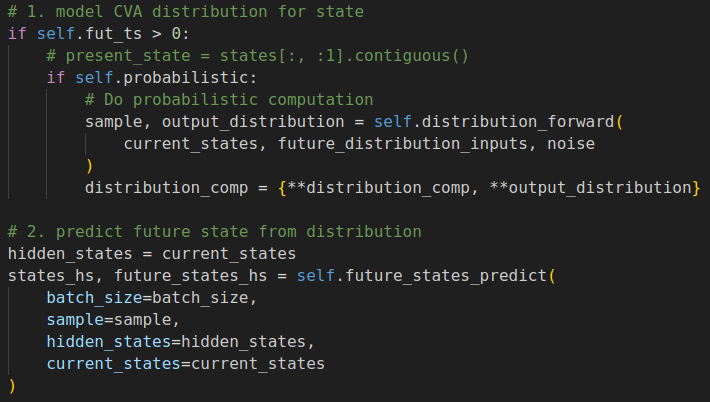
-
这边的self.predict_model函数里包含了GRU的实现,但是从代码上看,没有按照T循环调用GRU,而是设计了一个4层(layer_num=4)的GRU模拟状态随时间的推演。
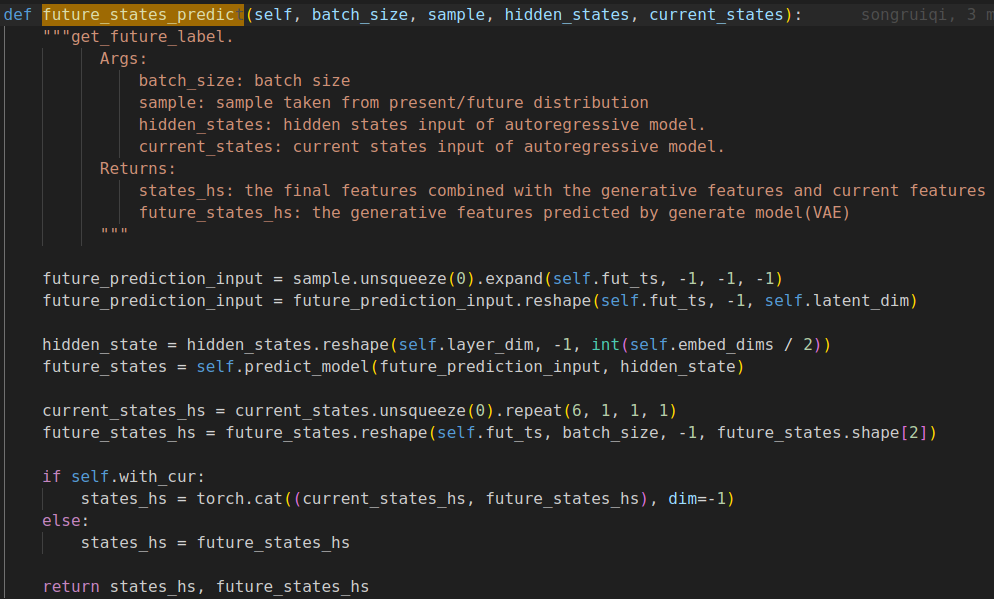
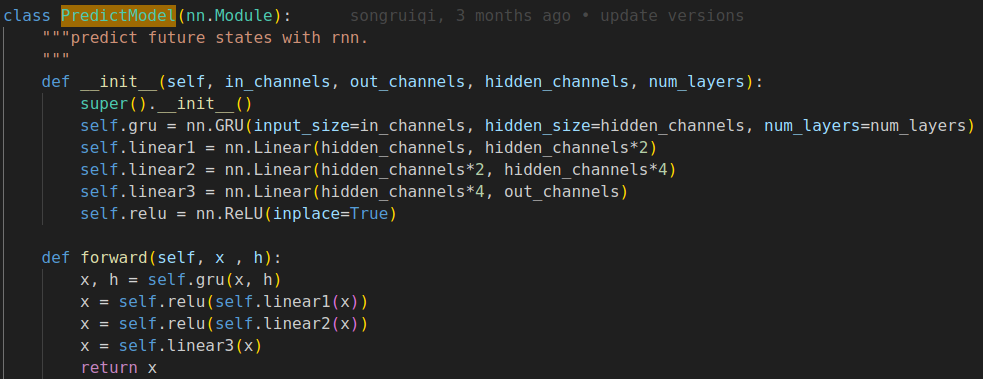
-
decoder是按照T循环解码出的轨迹点(下面的for循环),这里的self.ego_fut_decoder是个MLP,将GRU输出的latent future state转化为轨迹点
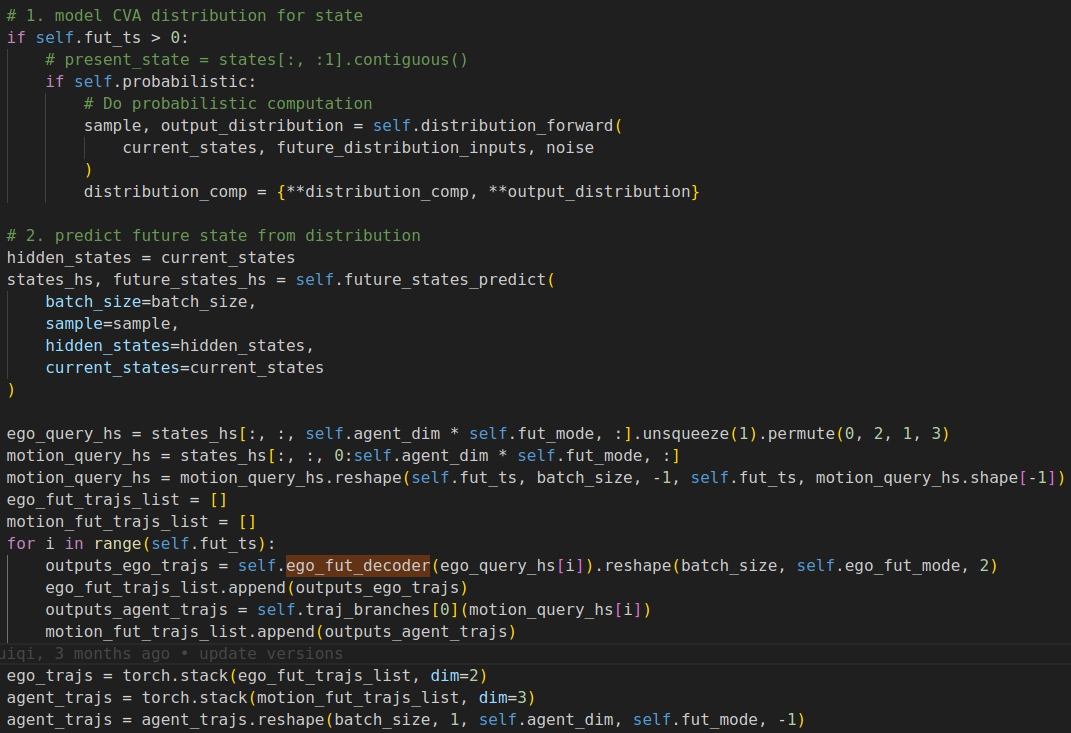
-
Generative End-to-End Autonomous Driving
-
轨迹loss
$$J_{prior}=L_{traj}(\hat{T_{e}},T_{e})+\frac{1}{N_{a}}L_{traj}(\hat{T_{a}},T_{a})+\lambda_{c}L_{focal}(\hat{C_{a}},C_{a})$$
- \(L_{traj}()\)衡量两条轨迹的L1 loss。 \(N_{a}\)是agent的数量, \(C_{a}\)是agent的预测类别, \(T_{a}\)是agent的预测轨迹。
-
将上面得到的instance tokens \(I\)通过encoder \(e_{i}\)映射到latent space \(Z\),也类似地输出一组输出一组 \(\mu_{i}\)和 \(\sigma_{i}\)。
-
\(e_{i}\)代码实现:
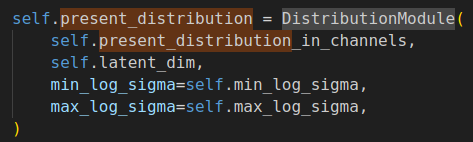
$$p(z|I)\thicksim N(\mu_{i},\sigma_{i})$$
-
-
通过KL散度衡量 \(p(z|I)\)和GT轨迹 \(p(z|\mathsf{\mathbf{T}}(T,f))\)之间的差异
$$J_{plan}=D_{KL}(p(z|I),p(z|\mathsf{\mathbf{T}}(T,f)))$$
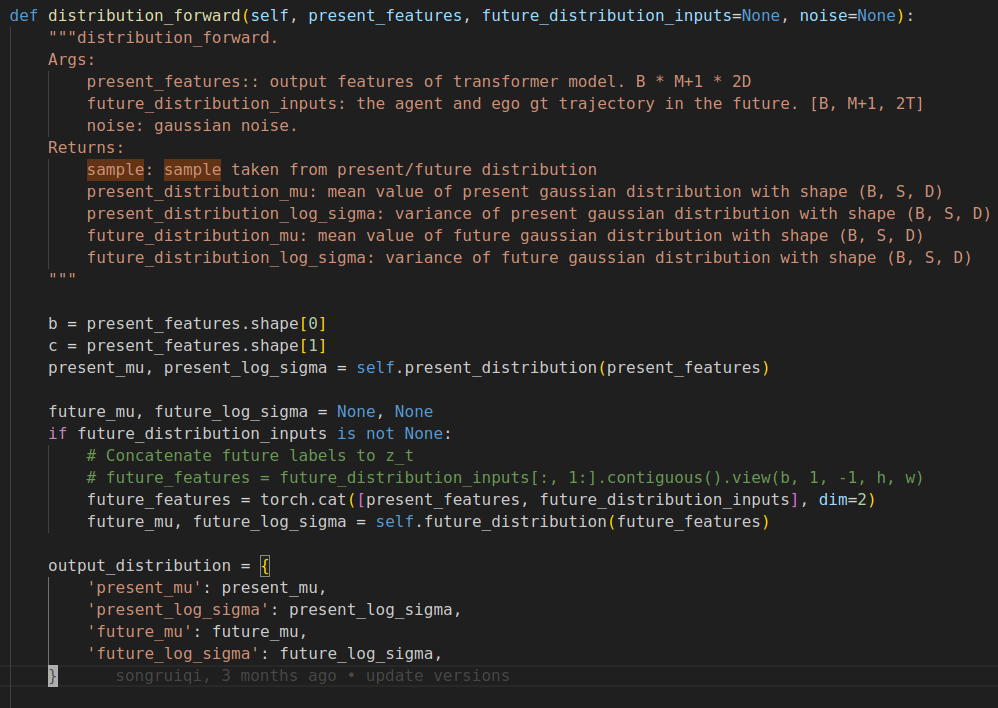
- KL散度衡量的就是上面的output_distribution中present和future的分布差异
-
总loss
$$J_{GenAD}=J_{prior}+\lambda_{plan}J_{plan}+\lambda_{map}J_{map}+\lambda_{det}J_{det}$$
-
在infer阶段,弃用future trajectory encoder(因为没有GT),从 \(p(z|I)\)中采样latent state,作为轨迹生成模块的输入