DiffusionDrive: Truncated Diffusion Model for End-to-End Autonomous Driving
背景知识
条件扩散模型
forward diffusion process
- 不断往采样出来的数据上增加噪声
$$q(\tau^{i}|\tau^{0})=\mathcal{N}(\tau^{i};\sqrt{\bar{\alpha}^{i}}\tau^{0},(1-\bar{\alpha}^{i})I)$$
- 其中 \(\tau^{0}\)是未添加噪声的初始采样数据, \(\tau^{i}\)是第 \(i\)次添加噪声后的数据
- \(\bar{\alpha}^{i}=\prod_{s=1}^{i}\alpha^{s}=\prod_{s=1}^{i}(1-\beta^{s})\), \(\beta^{s}\)是noise schedule
reverse diffusion process
- 训练一个噪声去除模型 \(f_{\theta}(\tau^{i},z,i)\)一步一步从 \(\tau^{i}\)再还原到 \(\tau^{0}\), \(\theta\)是训练模型的参数。
- 还原的过程中输入环境信息 \(z\)作为指导(条件),使得最终还原出来的 \(\tau^{0}\)和周围的环境有合理的交互
$$p_{\theta}(\tau^{0}|z)=\int p(\tau^{T})\prod_{i=1}^{T}p_{\theta}(\tau^{i-1}|\tau^{i},z)d\tau^{1:T}$$
预备实验
改造Transfuser为生成式模型
- 将transfuser模型最后的MLP回归层替换为conditional diffusion model。
- 将一个随机初始化的noise采样通过20次reverse diffusion操作refine为一条精细的轨迹。
- 实验证明diffusion模型的结果比MLP回归模型的更好。
模态坍缩
- 为了探索驾驶行为的多模特性,采样了20个随机噪声(满足高斯分布),通过20次reverse diffusion进行去噪。
- 结果20个随机采样的噪声最后都收敛到了一个模态。
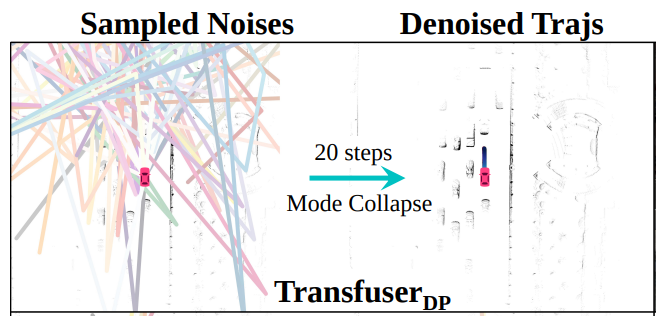
- 为了定量分析模态坍缩的现象,定义了一个模态多样性得分\(D\)(通过计算每条去噪后的轨迹和所有去噪后轨迹的平均重叠面积计算)
$$D=1-\frac{1}{N}\sum_{i=1}^{N}{\frac{Area(\tau_{i}\cap \bigcup_{j=1}^{N}\tau_{j})}{Area(\tau_{i}\cup \bigcup_{j=1}^{N}\tau_{j})}}$$
- \(\tau_{i}\)表示第 \(i\)条去噪轨迹, \(N\)是采样轨迹总数, \(\bigcup_{j=1}^{N} \tau_{j} \)是所有去噪轨迹的并集。
去噪开销
- DDIM diffusion模型需要20次去噪将一个随机噪声refine为可用的轨迹,导致计算负担非常大,无法在实车上部署。
模块细节
截断扩散模型
- 人类驾驶是有一定的固定范式的,没必要从一个完全随机的噪声开始去噪,因此,本文提出的方案尝试从anchored Gaussian distribution开始进行去噪过程。而不是从一个标准的高斯分布(随机噪声)开始去噪。
训练过程
- 通过K-means算法将训练集中自车行驶的轨迹进行聚类,得到20条anchors \(\lbrace a_{k}\rbrace_{k=1}^{N_{anchor}}\),其中 \(a_{k}=\lbrace (x_{t},y_{t})\rbrace_{t=1}^{T_{f}}\)
- 向anchor添加噪声:
$$\tau_{k}^{i}=\sqrt{\bar{\alpha}^{i}}a_{k}+\sqrt{1-\bar{\alpha}^{i}}\epsilon,\epsilon \in \mathcal{N}(0,I)$$
- 其中 \(i \in [1,T_{trunc}],T_{trunc}\ll T\)是扩散步数
- diffusion decoder \(f_{\theta}\)输入带噪声的anchor轨迹 \(\lbrace \tau_{k}^{i}\rbrace_{k=1}^{N_{anchor}}\),输出分类score \(\lbrace{s_{k}}\rbrace_{k=1}^{N_{anchor}}\)和去噪轨迹 \(\lbrace\tau_{k}\rbrace_{k=1}^{N_{anchor}}\)
$$\lbrace \lbrace s_{k},\tau_{k}\rbrace\rbrace_{k=1}^{N_{anchor}}=f_{\theta}(\lbrace \tau_{k}^{i}\rbrace_{k=1}^{N_{anchor}},z)$$
- 其中, \(z\)表示条件信息。
- 将带噪轨迹中最接近GT的轨迹的分类标签设置为true( \(y_{k}=1\)),其他为false( \(y_{k}=0\)),loss设计如下:
$$L=\sum_{k=1}^{N_{anchor}}{[y_{k}L_{rec}(\tau_{k},\tau_{gt})+\lambda BCE(s_{k},y_{k})]}$$
- 其中, \(\lambda\)用来平衡L1 reconstruction loss \(L_{rec}\)和binary cross-entropy classification loss
推理过程
- 去噪过程中,前一步去噪得到的轨迹作为输入传入下一步去噪过程,得到新的分类score \(\lbrace s_{k}\rbrace_{k=1}^{N_{anchor}}\)和去噪轨迹 \(\lbrace \tau_{k}\rbrace_{k=1}^{N_{anchor}}\)。
- 新的去噪轨迹 \(\lbrace \tau_{k}\rbrace_{k=1}^{N_{anchor}}\)会通过DDIM的更新规则采样轨迹给到下一步去噪过程。
算法架构
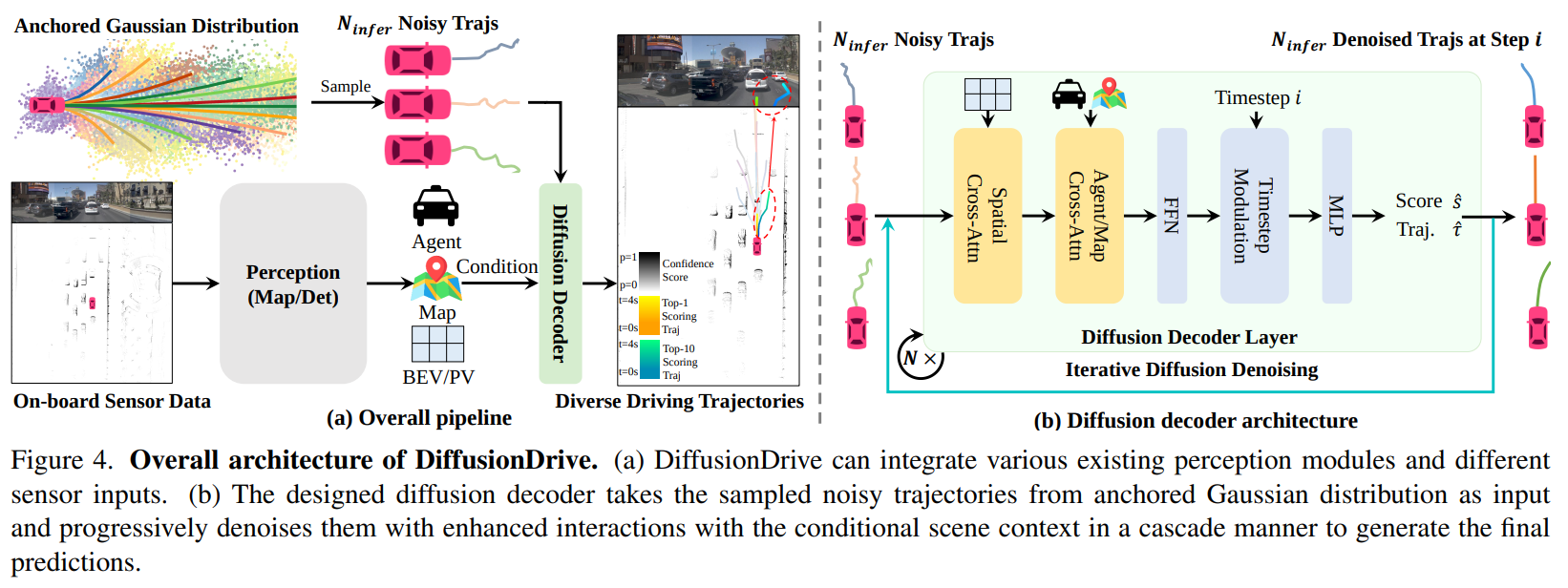
Diffusion decoder
- 给定一组符合anchored Gaussian distribution的带噪轨迹 \(\lbrace \tau_{k}\rbrace_{k=1}^{N_{infer}}\),通过 deformable spatial cross-attention将其与BEV和PV feature进行交互,得到trajectory feature。
- 将trajectory feature和感知模块中得到的agent/map query进行cross-attention。
- 为了对diffusion timestamp进行编码,引入Timestep Modulation layer
- 最后跟两个MLP,得到confidence score和trajectory offset(用上一层轨迹加上这个offset得到新的轨迹)
- 不同的diffusion decoder层共用一套模型参数
实验细节
- 在diffusion decoder层,只和BEV feature进行spatial cross-attention。由于transfuser模型没有map construction结果,只和agent query进行cross-attention。
- 采样20个anchor
- 通过2层diffusion decoder进行轨迹去噪。
- diffusion schedule 定为50/1000。