looyifan / Lagrangian Relaxation

Created Wed, 02 Apr 2025 10:32:39 +0800 Modified Wed, 02 Apr 2025 19:05:29 +0800
1716 Words

问题形式

  • 原问题：\(min_{x}f(x)\)，\(s.t.Ax=b\)，其中\(f(x)\)是个凸函数
  • 原问题的Lagrangian：\(L(x,\lambda):=f(x)+\langle\lambda,Ax-b\rangle\)，后面的尖括号是内积的操作符
  • 显然：\(max_{\lambda}f(x)+\langle\lambda,Ax-b\rangle= \lbrace\begin{matrix}f(x),&Ax=b \\ \infty,&otherwise\end{matrix} \)
  • 因此，原问题等于：\(min_{x}f(x),s.t.Ax=b\Leftrightarrow min_{x}max_{\lambda}L(x,\lambda)\)
  • 几何解释
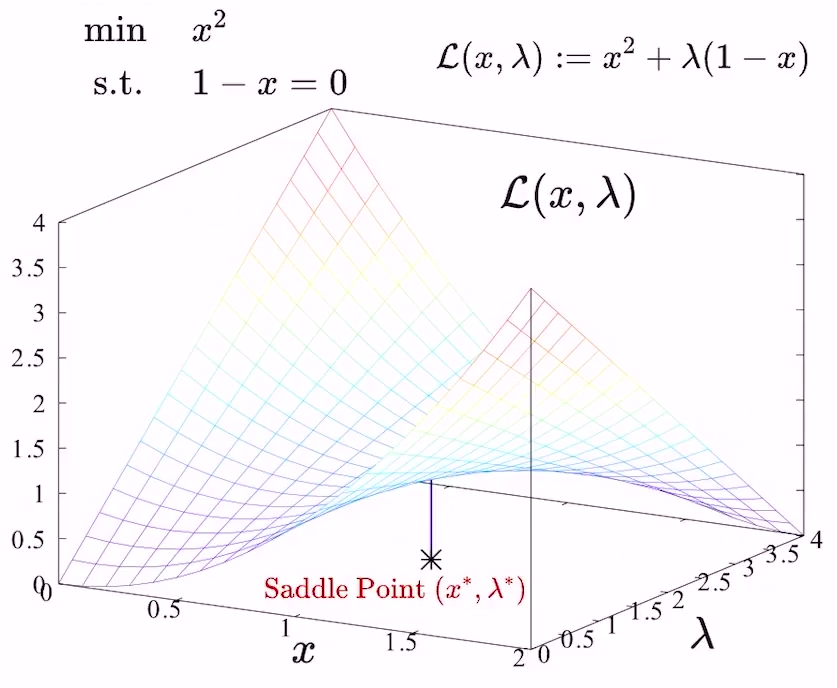
    • lagrangian geometry
    • 最优解即Lagrangian函数的鞍点
    • 从上图可以看到，\(x>1\)时，\(\lambda\)取无穷大，即可让Lagrangian函数趋于无穷大；\(x<1\)时，\(\lambda\)取负无穷大，即可让Lagrangian函数趋于无穷大；只有当\(x=1\)时，\(\lambda\)无论取什么值，Lagrangian函数的值都保持在一个上界之下

Uzawa’s Method

  • 推导过程
    • \(min_{x}max_{\lambda}L(x,\lambda):=f(x)+\left<\lambda,Ax-b\right>\)的后半部分\(max_{\lambda}L(x,\lambda):=f(x)+\left<\lambda,Ax-b\right>\)的取值是\(f(x)\)或\(\infty\)，即对于前面的\(x\)来说，Lagrangian函数是不连续的，导致这个min问题很难求
    • 现在假设我们把min和max交换一下顺序，\(max_{\lambda}min_{x}L(x,\lambda):=f(x)+\left<\lambda,Ax-b\right>\)，并且，如果后半部分\(min_{x}L(x,\lambda):=f(x)+\left<\lambda,Ax-b\right>\)是严格凸的话，给定一个\(\lambda\)就可以很轻易的求解\(x^{*}\)
    • 注意！von Neumann提到：\(max_{\lambda}min_{x}L(x,\lambda)\leq min_{x}max_{\lambda}L(x,\lambda)\)，当且仅当\(f(x)\)连续且凸时取等号
    • 因此我们直接通过梯度上升法求解对\(\lambda\)做maximize的对偶问题：\(d(\lambda):=min_{x}f(x)+\left<\lambda,Ax-b\right>\)
      • 由于每确定一个\(\lambda\)，都可以求得一个确定的\(x^{*}\)，所以\(x^{*}\)的值本质上是关于\(\lambda\)的函数，因此上面的对偶问题又可以写成\(d(\lambda)=L(x^{*}(\lambda),\lambda)\)
      • 我们将它对\(\lambda\)求导，\(\frac{\partial d}{\partial\lambda}=\frac{\partial L}{\partial x^{*}}\cdot\frac{\partial x^{*}}{\partial\lambda}+\frac{\partial L}{\partial\lambda}\)，注意\(\frac{\partial L}{\partial x^{*}}\)就是0，对于凸函数来说，导数为0的点就是最优解所在的点，所以\(\frac{\partial d}{\partial\lambda}=\frac{\partial L}{\partial\lambda}|_{x^{*}(\lambda)}\)，也就说，我们给定一个\(\lambda\)，可以确定一个最优的\(x^{*}\)，然后用\(x^{*}\)求得\(\frac{\partial d}{\partial\lambda}=Ax^{*}-b\)后，通过梯度上升求得新的\(\lambda\).
      • 总结一下，迭代步骤如下：
        • $$\lbrace \begin{matrix}x^{k+1}=argmin_{x}L(x,\lambda^{k}) \\ \lambda^{k+1}=\lambda^{k}+\alpha(Ax^{k+1}-b)\end{matrix}$$
        • \(\alpha\)是沿梯度方向前进的步长
  • 缺陷
    • (致命)该方法要求\(f(x)\)是凸的
    • (致命)该方法要求\(min_{x}L(x,\lambda):=f(x)+\left<\lambda,Ax-b\right>\)关于原问题的优化变量\(x\)是严格凸的
    • 梯度上升的步长需要调参
    • 收敛速度不一定快，因为严格凸不保证函数的光滑性，如果函数不光滑，在某些点就只存在次梯度，根据前面的介绍，沿着次梯度的反（正）方向走不保证函数值下降（上升）。