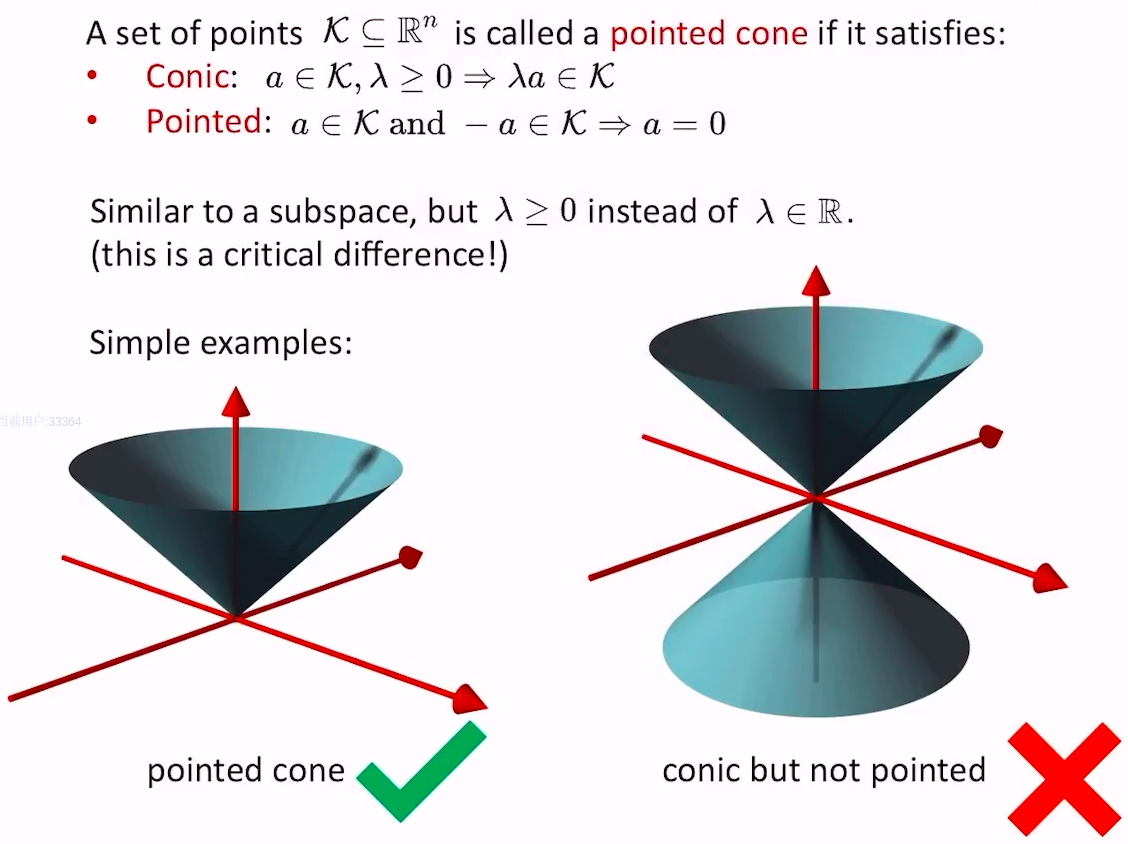
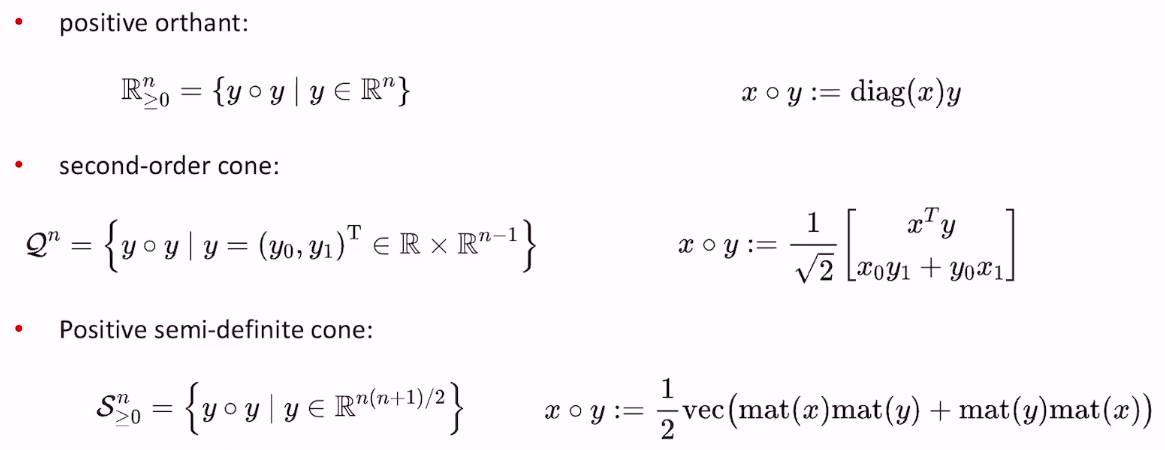锥的定义
- 常见的几种Cone
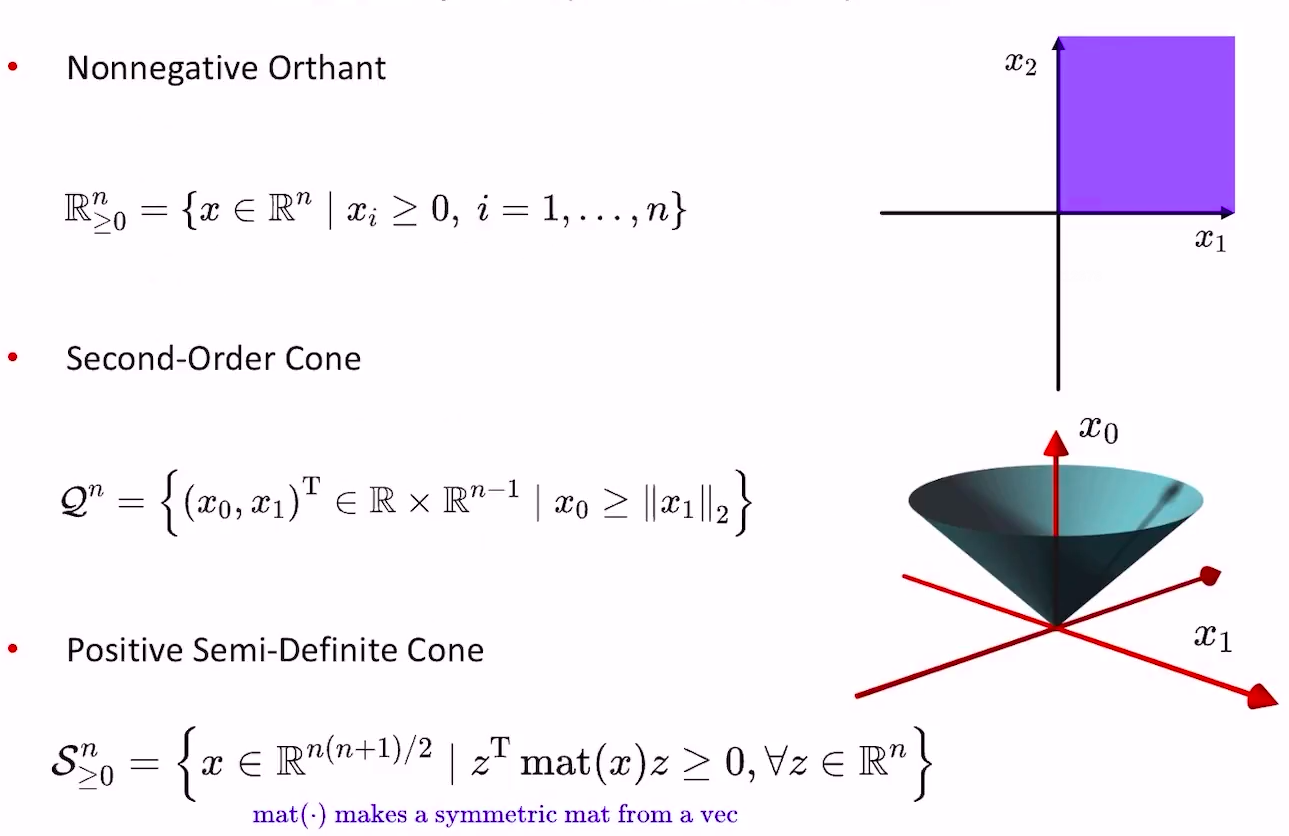
- Nonnegative Orthant通过仿射变换可以变成线性规划LP
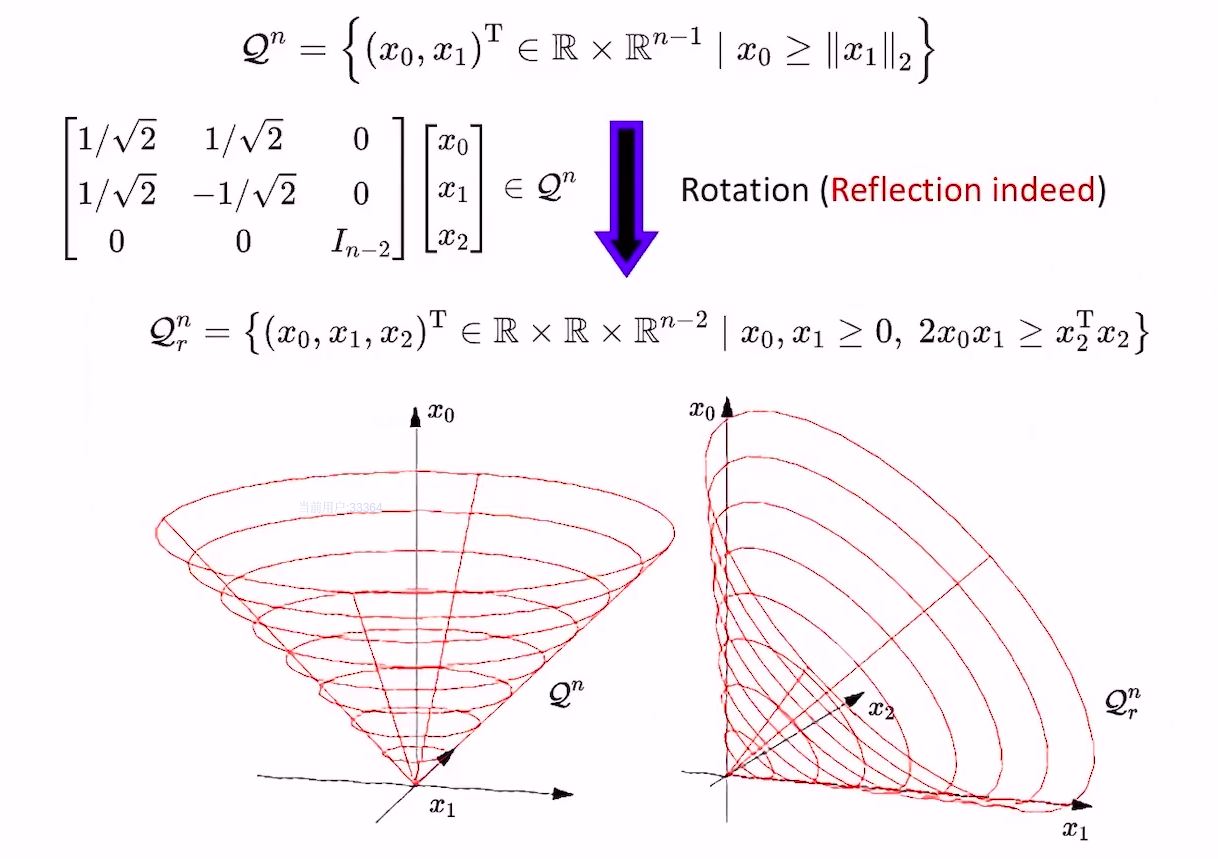
- Second Order Cones
- Rotatted Second Order Cones(本质上是个反射变换,不是旋转)
- Symmetric Cones
- 定义
- 一个锥是对称锥,当且仅当其可以表达为一个平方操作\( \lbrace x^{2}:=x\circ x|x\in\mathbb{R}^{n}| \rbrace \)
- 其中,\(\circ\)操作需要满足如下性质
- \(x\circ%20y\)是bilinear的
- \(x\circ%20y=y\circ%20x\)
- \(x^{2}\circ(y\circ%20x)=(x^{2}\circ%20y)\circ%20x\)
- \(\langle x, y\circ z\rangle = \langle x\circ y,z\rangle\)
- \((\mathbb{R}^{n},\circ)\)所表示的这样一个集合被称为Euclidean Jordan algebra
- 上面三种锥都是对称锥(因为都可以转化为平方的形式)

- 具体来说,上面三种对称锥,各自的\(\circ\)操作的定义也是不一样的
- 定义
Spectral Decomposition
- 每个Euclidean Jordan algebra都有它的谱分解\(x=\sum_{i=1}^{\theta}\lambda_{i}q_{i}\),其中,\(\lambda_{i}\)是特征值,\(q_{i}\)是特征向量
- Euclidean Jordan algebra的谱分解具有如下性质
- $$q_{i}^{2}=q_{i}$$
- $$q_{i}\circ q_{j(\neq i)}=0$$
- 由此我们可以推得
- 特征向量是互相正交的
- $$\langle q_{i}\circ q_{j(\neq i)} \rangle =\langle q_{i}\circ q_{i},q_{j(\neq i)}\rangle =\langle q_{i},q_{i}\circ q_{j(\neq i)}\rangle =0$$
- 一个向量属于一个对称锥,当且仅当他的所有特征值都是非负的
- 当所有特征值都是正数时,向量在对称锥的内部(不包含边界)
- 特征向量是互相正交的
- 典型对称锥的谱分解
- positive orthant
- $$\lambda_{i}=x_{i}$$
- $$q_{i}=e_{i}$$
- second-order cone
- $$\lambda_{i}=\frac{x_{0}\pm\left|x_{1}\right|_{2}}{\sqrt{2}}$$
- $$q_{i}=\frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ \pm x_{1}/\left|x_{1}\right|_{2} \end{bmatrix}$$
- positive semi-definite cone
- \(\lambda_{i}=\lambda_{i}\),\(q_{i}=vec(v_{i}v_{i}^{T})\),其中\(\lambda_{i}\)和\(v_{i}\)是\(mat(x)\)的特征值和特征向量
- positive orthant
对偶锥
- 定义
- 一个锥\(\kappa\)的对偶锥的定义如下
- $$\kappa^{*}=\lbrace x|\langle x,y\rangle \geq 0, \forall y\in \kappa | \rbrace$$
- 对称锥的对偶锥是它本身
- 一个锥\(\kappa\)的对偶锥的定义如下
优化问题的转化

- QP问题的优点是可以解得很快,但缺点是有时会出错,但转化为SOCP问题后,求解的数值稳定性会更好

扩展
- 很多很难的优化问题,通过Lasserre hierarchy方法可以被构造成一个松弛问题(可以表达为SDP的形式)